Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.6 - Ex. 40
Encontre as assíntotas horizontal e vertical de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.
40.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é determinar as assíntotas horizontais e verticais e a partir delas, esboçar o gráfico da função.
Parece complicado?
Para acharmos as assíntotas, nós temos métodos particulares...
As assíntotas horizontais de uma função podem ser obtidas a partir dos limites
Já para determinar as assíntotas verticais, temos que analisar a função nas suas indefinições pois aqui a função tende a , ou seja, em outras palavras, temos que encontrar de modo que
Veja só!
Passo 2
Começaremos com a assíntota horizontal, temos que fazer:
Se der um número real, a assíntota será esse número. Caso dê infinito não teremos assíntota horizontal. Vamos para o cálculo!
Aplicando o limite na função, temos
Podemos colocar em evidencia no numerador e no denominador para simplificar a fração
Simplificando temos
O limite de uma constante é igual a própria constante. Já os limites de e serão iguais a já que temos números relativamente pequenos sendo divididos por números muito grandes
Substituindo tudo para dentro do limite, temos isso aqui:
Então, temos assíntota horizontal para positivo e é a reta
Vamos reutilizar o limite
Para
Nesse caso, a mesma análise que fizemos para serve para ...
Os termos e tendem a , assim
Então, temos uma assíntota horizontal dada por
Tranquilo até aqui?
Passo 3
Agora, partiremos para a assíntota vertical...
Como vimos no passo 1, deve tender a ou . Isso acontece em uma fração quando o denominador se aproxima de a medida que o numerador não se aproxima...
Vamos aplicar o limite do passo 1
Os valores de que anulam o denominador , e :
Então os possíveis valores de são , e
é raiz tanto do numerador quanto do denominador, Então a função está definida em , logo, não nos preocuparemos com ela para fazer as assíntotas.
Vamos apenas fazer uma pequena manipulação no limite para facilitar nossos cálculos
Simplificando o primeiro limite...
Para , temos
Perceba que como tende a , o termo tende a um número muito grande, quase infinito, da mesma forma a fração .
Porém, nesse último o sinal importa, então se , o termo tende a , mas se , o termo tende a .
Portanto, temos
Dessa forma a reta é uma assíntota vertical.
Bacana, não é?
Passo 4
Agora vamos analisar o que acontece para
Temos que para e próximo de , é positivo e é positivo.
Então para pontos à direita de :
Para e próximo de 1, é positivo e é negativo.
Então para pontos á esquerda de :
A reta é assíntota vertical.
A partir das assíntotas, podemos esboçar o gráfico de como
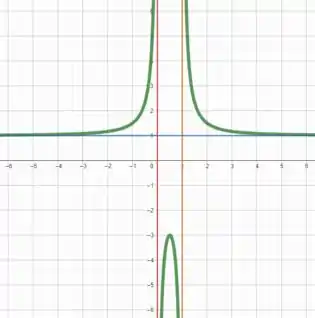
E aí! entendeu tudo? Responde Aí!
Resposta
É uma assíntota horizontal.
São as assíntotas verticais.