Exercícios de Assíntota Horizontal e Vertical - Lista de Exercícios Resolvida
Questão 1
Seja . Determine o que se pede, justificando adequadamente o que não há.
Domínio de .
Assíntotas horizontais e verticais da curva
Ver solução completaQuestão 2
Determine, caso existam, as assíntotas horizontais e verticais do gráfico da função abaixo
Ver solução completaQuestão 5
Determine, caso existam, as assíntotas horizontais e verticais do gráfico da função abaixo
Ver solução completaQuestão 6
Considere dada por:
- A função é contínua em ? Justifique sua resposta.
- Caso existam, encontre as assíntotas horizontais e verticais de .
Questão 7
Questão 1.3 - A função terá duas assíntotas horizontais distintas se e somente se
(a) e .
(b) e .
(c) e .
(d) e .
Ver solução completaQuestão 8
Encontre, se existirem, as assíntotas horizontas e verticais do gráfico da função.
Ver solução completaQuestão 9
Encontre, se existirem, as assíntotas horizontas e verticais do gráfico da função.
Ver solução completaQuestão 10
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 11
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 13
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 18
3. Calcule as assíntotas horizontais e verticais das seguintes funções
f.
Ver solução completaQuestão 19
3. Calcule as assíntotas horizontais e verticais das seguintes funções
h.
Ver solução completaQuestão 20
3. Calcule as assíntotas horizontais e verticais das seguintes funções
i.
Ver solução completaQuestão 21
3. Calcule as assíntotas horizontais e verticais das seguintes funções
b.
Ver solução completaQuestão 22
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 23
Questão 3: Seja dada por
b) Encontre a assíntota horizontal de quando . Existe assíntota vertical em algum ponto?
Ver solução completaQuestão 24
1) Considere
Sejam a assíntota vertical e a assíntota horizontal ao gráfico de . As retas e se interceptam no ponto . Então é igual a:
Questão 25
Seja . Determine o que se pede, justificando adequadamente o que não há.
Domínio de .
Assíntotas horizontais e verticais da curva
Ver solução completaQuestão 26
3. Calcule as assíntotas horizontais e verticais das seguintes funções
c.
Ver solução completaQuestão 27
3. Calcule as assíntotas horizontais e verticais das seguintes funções
b.
Ver solução completaQuestão 32
Considere a função
Determine todas as assíntotas verticais e horizontais ao gráfico de
Ver solução completaQuestão 33
Encontre as assíntotas horizontais e verticais, caso existam, da função
Ver solução completaQuestão 34
Esboce o gráfico e de um exemplo de uma função que satisfaça todas as seguintes condições dadas: , .
Ver solução completaQuestão 35
Sejam e números reais tais que a reta é uma assíntota horizontal da função
.
O valor de é
Ver solução completa
Questão 36
- Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
k.
Ver solução completaQuestão 37
Considere a função , definida para todo com .
Determine as assíntotas verticais do gráfico de , se houver tais.
Determine as assíntotas horizontais do gráfico de , de houver tais.
Determine os intervalos de crescimento e decrescimento da função . Determine ainda os pontos de máximo e de mínimo de (se houver); especifique ainda se tais pontos são globais (absolutos) ou locais (relativos).
Determine os intervalos de concavidade para cima e para baixo do gráfico de , assim como seus pontos de inflexão (se houver).
Usando as informações obtidas nos itens anteriores, esboce o gráfico de . Deve incluir as assíntotas (se houver), e deve marcar os pontos notáveis obtidos junto com suas coordenadas.
Ver solução completaQuestão 39
3. Calcule as assíntotas horizontais e verticais das seguintes funções
e.
Ver solução completaQuestão 40
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 41
- Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
k.
Ver solução completaQuestão 42
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 43
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 44
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 45
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 46
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 47
52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
b)
Ver solução completaQuestão 48
52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
a)
Ver solução completaQuestão 50
Considere a função , definida em seu maior domínio possível.
b) Determine, caso existam, as assíntotas verticais do gráfico de e os limites laterais nessas assíntotas.
Ver solução completaQuestão 51
Considere a função , definida em seu maior domínio possível.
a) Determine os limites no infinito e, caso existam, as assíntotas horizontais do gráfico de .
Ver solução completaQuestão 52
14) Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 54
12) Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 55
Determine as assíntotas horizontais e verticais, se existir, do gráfico da função .
Ver solução completaQuestão 56
Em Física, é comum que se peça para analisar movimentos desprezando o atrito, o que é uma boa aproximação em muitos casos. Em diversas situações, no entanto, é necessário levar o atrito do ar, por exemplo, em conta. O modelo mais simples para o atrito em um fluido é aquele no qual se assume que a força de atrito a cada instante de tempo sobre um ponto material é proporcional à sua velocidade naquele instante. Em um modelo assim, pode-se mostrar que o módulo da velocidade de um objeto em queda próximo à superfície da Terra caindo do repouso e sujeito ao atrito com o ar varia com o tempo t de acordo com a função
em que é a massa do objeto, é a aceleração da gravidade, e é uma constante de proporcionalidade com dimensões de . Nessa situação, se o objeto pudesse cair indefinidamente, sua velocidade se aproximaria de um certo valor constante, chamado de velocidade terminal. No gráfico de , essa velocidade é representada por uma assíntota horizontal. Qual é ela?
Ver solução completaQuestão 57
3. Calcule as assíntotas horizontais e verticais das seguintes funções
d.
Ver solução completaQuestão 58
3. Calcule as assíntotas horizontais e verticais das seguintes funções
j.
Ver solução completaQuestão 59
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Questão 61
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota horizontal ao gráfico de ? Em caso afirmativo, obtenha as equações
das assíntotas horizontais ao gráfico de .
Ver solução completaQuestão 62
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
i)
- Existe assíntota vertical ao gráfico de ? Em caso afirmativo, obtenha as equações das assíntotas verticais ao gráfico de .
Questão 63
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
i)
- Existe assíntota horizontal ao gráfico de ? Em caso afirmativo, obtenha as equações das assíntotas horizontais ao gráfico de .
Questão 64
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota vertical ao gráfico de ? Em caso afirmativo, obtenha as equações das assíntotas verticais ao gráfico de .
Ver solução completaQuestão 65
Q04) Encontre as assíntotas horizontais e verticais da seguinte função
Ver solução completaQuestão 66
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota horizontal ao gráfico de ? Em caso afirmativo, obtenha as equações
das assíntotas horizontais ao gráfico de .
Ver solução completaQuestão 67
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota vertical ao gráfico de ? Em caso afirmativo, obtenha as equações das assíntotas verticais ao gráfico de .
Ver solução completaQuestão 68
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota horizontal ao gráfico de ? Em caso afirmativo, obtenha as equações
das assíntotas horizontais ao gráfico de .
Ver solução completaQuestão 70
- Considere a dada por e suas derivadas e
- Obtenha se houver, as assíntotas de .
Ver solução completaQuestão 71
Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas
e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos
à assíntota para, em seguida, checar se cada um deles é de fato assíntota.
Ver solução completaQuestão 72
Explique o que significa dizer que a reta y = L é uma assíntota horizontal da função f.
Em seguida, considerando os gráficos esboçados no Exercício 1, determine as assíntotas
horizontais sugeridas por cada um deles.
Ver solução completaQuestão 74
Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas
e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos
à assíntota para, em seguida, checar se cada um deles é de fato assíntota.
Ver solução completaQuestão 76
Calcular assíntota verticais não é o mesmo que igualar denominadores a zero! Por exemplo, o denominador da função se anula em , mas
e, portanto, x = 2 não é assíntota vertical. Para as funções abaixo, determine os candidatos
à assíntota para, em seguida, checar se cada um deles é de fato assíntota.
Ver solução completaQuestão 77
Calcule as assíntotas horizontais e verticais da função abaixo, se existirem. Caso não existam, justifique sua resposta.
Ver solução completaQuestão 78
Calcule as assíntotas horizontais e verticais da função abaixo, se existirem. Caso não existam, justifique sua resposta.
Ver solução completaQuestão 79
Calcule as assíntotas horizontais e verticais da função abaixo, se existi- rem. Caso não existam, justifique sua resposta.
Ver solução completaQuestão 80
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Questão 81
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Questão 82
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que
se pede:
Existe assíntota vertical ao gráfico de g(x)? Em caso afirmativo, obtenha as equações das assíntotas verticais ao gráfico de g(x).
Ver solução completaQuestão 83
Seja .
- Determine os intervalos de crescimento/decrescimento de e os seus pontos de máximo/mínimo locais.
- Determine os intervalos onde é côncava para cima/baixo e os seus pontos de inflexão.
- Caso existam, encontre as assíntotas horizontais e verticais de .
- Esboce o gráfico de usando (pelo menos) as informações obtidas nos itens (a), (b) e (c).
Questão 84
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 85
Considerando a função
definida para , resolva os itens abaixo.
(a) Calcule os limites no infinito da função e, em seguida, determine a(s) assíntota(s)
horizontal(is) do gráfico da função , se esta(s) existir(em).
(b) Calcule os limites laterais de no ponto e, em seguida, determine a(s)
assíntota(s) vertical(is) do gráfico da função , se esta(s) existir(em).
(c) Faça um esboço do gráfico de .
Ver solução completaQuestão 87
7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.
b)
Ver solução completaQuestão 89
7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.
a)
Ver solução completaQuestão 90
7.6 Para as funções abaixo, determine quais admitem uma assíntota vertical. Inclua as equações e os gráficos das assíntotas, bem com um esboço dos gráficos dessas funções, indicando o(s) comportamento(s) assintóticos perto da(s) assíntotas.
c)
Ver solução completaQuestão 92
Determine o valor de para que a função definida por
Seja continua. Para os valores de achados:
- possui assíntotas horizontais quando ?
- possui assíntotas verticais?
Questão 93
Considere a seguinte função e suas derivadas:
, ,
Calcule as assíntotas de , estude o sinal da primeira e segunda derivada, indique os pontos de máximo/mínimo locais, os pontos de inflexão, e faça um esboço de
Ver solução completaQuestão 94
Dê exemplos de funções com assíntotas (dois exemplos para cada tipo).
Ver solução completaQuestão 95
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 96
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 97
3. Calcule as assíntotas horizontais e verticais das seguintes funções
a.
Ver solução completaQuestão 99
Seja
(c) Caso existam, encontre as assíntotas horizontais e verticais de .
Ver solução completaQuestão 100
Seja
(c) Caso existam, encontre as assíntotas horizontais e verticais de .
Ver solução completaQuestão 101
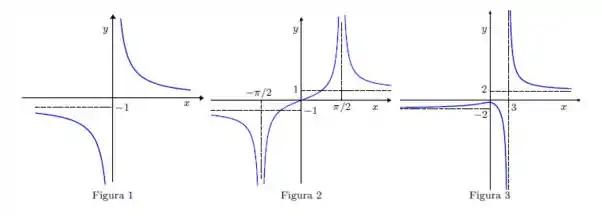
Explique o que significa dizer que a reta x = a é uma assíntota vertical da função . Em
seguida, considerando as funções esboçadas nos gráficos abaixo, determine as assíntotas verticais sugeridas por cada um deles.
Questão 102
Seja
(c) Caso existam, encontre as assíntotas horizontais e verticais de .
Ver solução completaQuestão 110
Seja
b) Encontre a assíntota horizontal de quando . Existe assíntota vertical em algum ponto?
Ver solução completaQuestão 115
Considere a função
Seja o conjunto de números reais tais que a reta é uma assíntota vertical de . Suponha que a soma dos elementos de é igual a 5. O valor de é
Questão 116
Seja a função
Determine o domínio e imagem de , bem como as ass ́ıntotas horizontais e verticais
do gráfico de (se existirem).
Ver solução completaQuestão 117
Encontre a assíntota horizontal de quando. Existe assíntota vertical em algum ponto?
Ver solução completaQuestão 121
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Determine a assíntota do gráfico de , usando a definição de assíntota. Em seguida, faça o esboço do gráfico.
Questão 122
13) Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Ver solução completaQuestão 123
Determine as assíntotas horizontais e verticais, caso existam, da função definida por:
Ver solução completaQuestão 124
Seja
- Determine o domínio da função
- Encontre as assíntotas verticais e horizontais da função . Calcule todos os limites necessários.
Questão 125
Resolva as seguintes questões:
- Explique por que a função não possui assíntotas verticais
Questão 127
Calcule as assíntotas horizontais e verticais das seguintes funções.
Ver solução completaQuestão 128
Calcule as assíntotas horizontais e verticais das seguintes funções.
Ver solução completaQuestão 129
Calcule as assíntotas horizontais e verticais das seguintes funções.
Ver solução completaQuestão 130
Calcule as assíntotas horizontais e verticais das seguintes funções.
Ver solução completaQuestão 131
51. Utilize limites para determinar as equações para todas as assíntotas verticais.
a)
Ver solução completaQuestão 132
51. Utilize limites para determinar as equações para todas as assíntotas verticais.
b)
Ver solução completaQuestão 133
51. Utilize limites para determinar as equações para todas as assíntotas verticais.
c)
Ver solução completaQuestão 134
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 135
1) Seja a função definida pela expressão:
Onde é um número positivo.
- Determine as assíntotas horizontais do gráfico de , caso elas existam
- Determine os valores de que tornam contínua no ponto
Questão 137
Seja satisfazendo a seguinte propriedade
Então podemos afirmar que:
- Existe tal que, para todo , temos
- está definida para todo
- Existe tal que, para todo , vale
- Existe tal que, para todo , vale
Questão 138
52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
c)
Ver solução completaQuestão 139
52. Utilize limites para determinar as equações para todas as assíntotas horizontais.
d)
Ver solução completaQuestão 140
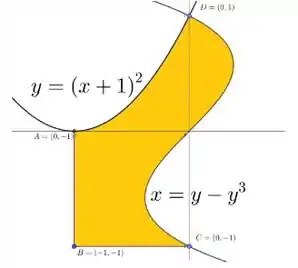
Observe a figura abaixo, a região hachurada é limitada pelas curvas e .
Escreva às integrais duplas necessárias para encontrar a área da região hachurada. Detalhe os pedaços de regiões utilizadas na sua decomposição.
Não é necessário calcular as integrais.
Questão 142
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
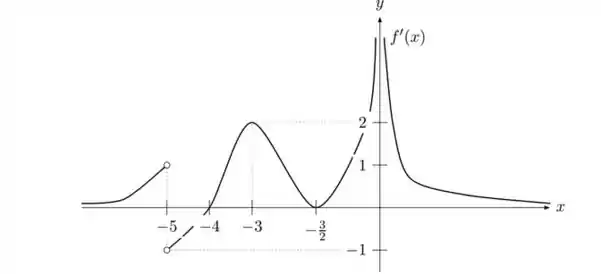
Responda, justificando, o que se pede:
As assíntotas verticais e horizontais, caso existam;
Ver solução completaQuestão 143
Questão: Considere a função
(a) Faça o estudo completo do comportamento desta função, ou seja, estude o comportamento assintótico, crescimento e decrescimento, concavidade, etc.
Ver solução completaQuestão 144
Para cada uma das funções abaixo, determine as assíntotas horizontais e verticais.
Ver solução completaQuestão 145
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gr��fico.
Ver solução completaQuestão 146
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.
Ver solução completaQuestão 147
Considere a função
d) Determine, caso existam, as assíntotas horizontais de .
Ver solução completaQuestão 148
Esboce o gráfico das funções abaixo e dê as equações das assíntotas, quando existirem
Parte 1: determine os pontos de máximos, mínimos, inflexão, bem como os intervalos das concavidades
Parte 2: determine as assíntotas (quando existirem) e o esboço do gráfico.
Ver solução completaQuestão 150
Considere . Sabendo que a assíntota vertical e assíntota horizontal do gráfico de se interceptam no ponto , o valor de é: