Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 10

Encontre o centroide da região.

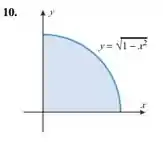
Passo 1

A ideia aqui é encontrar o centroide usando nossa fórmulinha:

overset(-)(x) = (1)/(á r e a d e R) int_a^b x ( f (x) - g (x) ) d x

overset(-)(y) = (1)/(á r e a d e R) int_a^b (1)/(2) [(f (x))^2 - (g (x))^2] d x

Passo 2

Vamos achar as coordenadas do centroide por integração. Primeiro a coordenada overset(-)(x) :

overset(-)(x) = (1)/(á r e a d e R) int_a^b x ( f (x) - g (x) ) d x

No eixo x nossa região está entre 0 e 1 , e no eixo y , nossa região está entre y = f (x) = sqrt(1 - x^2) (por cima) e y = g (x) = 0 (por baixo).

Como temos (1)/(4) de um círculo de raio 1 , a área é (pi)/(4) .

Nossa integral fica:

overset(-)(x) = (4)/(pi) int_0^1 x (sqrt(1 - x^2)) d x

Usando substituição simples:

overset(-)(x) = (4)/(3 pi)

Passo 3

Agora a coordenada overset(-)(y) :

overset(-)(y) = (1)/(á r e a d e R) int_a^b (1)/(2) [(f (x))^2 - (g (x))^2] d x

overset(-)(y) = (4)/(pi) int_0^1 (1)/(2) ((sqrt(1 - x^2))^2 - 0^2) d x

Elevando a função ao quadrado e calculando a integral de polinômios que aparecer:

overset(-)(y) = (4)/(3 pi)

Resposta

(overset(-)(x) , overset(-)(y)) = ((4)/(3 pi) , (4)/(3 pi))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral. ∫ 1 3 1 + 2 x - 4 x 3 d x
Calcule a integral. ∫ - 2 2 3 u + 1 2 d u
Calcule a integral. ∫ - 2 0 u 5 - u 3 + u 2 d u
Calcule a integral. ∫ 0 4 2 v + 5 3 v - 1 d v
Calcule a integral. ∫ - 1 0 2 x - e x d x