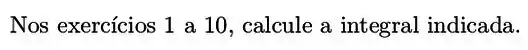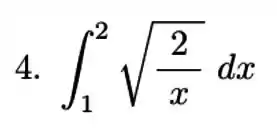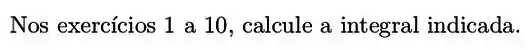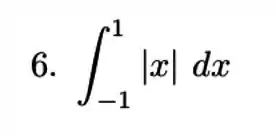Exercícios de Teorema Fundamental do Cálculo – Integral Definida - Lista de Exercícios Resolvida

Calcule a integral.

Calcule as integrais:

Calcule a integral.

Calcule a integral.

Calcule a integral

Calcule as integrais definidas abaixo

Calcule a integral

E esboce a região cuja área a integral representa.

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

A velocidade de queda de um corpo com massa caindo verticalmente após segundos pode ser modelada por

desde que suponhamos que a resistência do ar seja proporcional ao valor de , onde representa a aceleração gravitacional e é uma constante adimensional. Encontre a altura com relação a superfície da Terra, supondo que a altura inicial seja de metros.

Calcule

Considere contínua e a seguinte proposição:

Para todo então:

1. Dê uma exemplo para a proposição.
2. Decida se a proposição é falsa ou verdadeira.

O custo unitário (C), em dólares, para produção de um artigo científico em um periódico de circulação na Europa é modelado por

Sendo o tempo da circulação da revista. Calcule a integral dada para a verificação do custo unitário de cada artigo durante o período de meses.

Calcule as integrais

Considere a função . Determine a equação da reta tangente ao gráfico de no ponto

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

No exercício 1 da lista de exercícios 4.4 fizemos a substituição de variável e calculamos a integral indefinida.

Calcule agora a integral

de duas

formas:

(1) usando a integral indefinida e substituindo os índices e

(2) reescrevendo a integral definida na variável u.

Em cada item é dado um somatório de parcelas. Determine um intervalo e uma função f tais que o somatório dado seja a soma de Riemann de com subintervalos e com pontos amostrais nas extremidades direitas desses subintervalos.

c)

Seja a função definida por partes

Calcule

Seja . Então, é igual a

Considere:

Onde é a função cujo gráfico é dado abaixo:

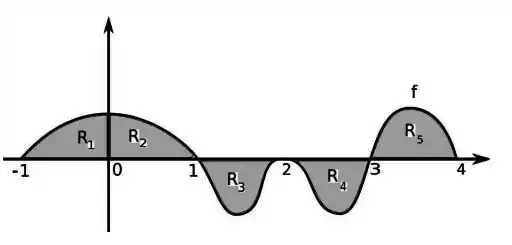
Sabendo que as áreas das regiões , , , e são:

.

Calcule , , , , e .

Sabendo que

Podemos concluir que é igual a

Estude a convergência de:

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

Use o Teorema Fundamental do Cálculo para calcular a integral.

2. Use o Teorema Fundamental do Cálculo para calcular a integral.

d)

2. Use o Teorema Fundamental do Cálculo para calcular a integral.

b)

2. Use o Teorema Fundamental do Cálculo para calcular a integral.

c)

Use o Teorema Fundamental do Cálculo para calcular a integral.

2. Use o Teorema Fundamental do Cálculo para calcular a integral.

e)

2. Use o Teorema Fundamental do Cálculo para calcular a integral.

f)

Seja a função a função definida por partes

Calcule

Calcule a integral.

d)

1. A função aceleração (em ) e a velocidade inicial (em ) são dadas para uma partícula movendo-se ao longo de uma reta. Encontre a velocidade no instante t e a distância percorrida durante o intervalo de tempo dado.

b. , e

1. A função aceleração (em ) e a velocidade inicial (em ) são dadas para uma partícula movendo-se ao longo de uma reta. Encontre a velocidade no instante t e a distância percorrida durante o intervalo de tempo dado.
   1. , e

Avalie a integral definida.

c.

Avalie a integral definida.

d.

Seja uma função contínua no intervalo , tal que

Calcule a integral

1) Calcule as integrais definidas abaixo.

b)

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Alguém me garantiu que a integral abaixo é verdadeira. Por quê?

Calcule as seguintes integrais

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

Calcule as integrais definidas abaixo

Calcule as integrais definidas

1) Calcule as integrais definidas abaixo.

c)

Calcule as integrais definidas

1) Calcule as integrais definidas abaixo.

a)

Calcule as integrais definidas

Calcule as integrais definidas abaixo

Seja um número positivo. Considere a integral definida dada a seguir

Pode-se afirmar que o valor da integral está correto se for igual a:

(a)

(b)

(c)

(d)

(e)

Selecione qual dos pontos abaixo pertence à reta tangente ao gráfico de no ponto , onde

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

Suponha que a velocidade mínima para que um objeto escape da força gravitacional da Terra seja dada por

onde representa a massa da Terra, a constante gravitacional de e a distância até o centro da Terra. Considere que no instante inicial , o raio da Terra, e mostre que e estão relacionados pela equação

onde é a velocidade inicial.

Se é uma função contínua e não negativa em , então a integral é exatamente a área da região do gráfico de e acima do eixo . Utilizando o gráfico da função, calcule cada uma das integrais abaixo

Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2

Expresse em termos de uma integral, o deslocamento de um objeto entre os instantes de tempo e , sabendo que sua função velocidade é .

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Calcule as integrais definidas abaixo. Sugestão: você já resolveu essas integrais indefinidas no exercício 2 da lista de exercícios 4.6

Avalie a integral definida.

a.

Avalie a integral definida.

b.

Calcule as integrais definidas abaixo

Calcule a integral.

c)

Use o Teorema Fundamental do Cálculo para calcular a integral.

g)

Calcule a integral.

b)

Calcule a integral.

Seja uma função cuja derivada é . Explique integral definida usando e .

. Seja dada por , se e . Se então o valor da integral é:

Escolha uma opção:

Calcule as integrais definidas abaixo