Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 29
Encontre as dimensões do triângulo isósceles de maior área que pode ser inscrito em um círculo de raio .
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
O enunciado nos deu um triângulo isósceles inscrito dentro de uma circunferência de raio e pediu pra gente encontrar a maior área possível desse triângulo.
Por dimensões do triângulo, entendemos como base e altura máximos. A única informação que o enunciado nos dá, é que o raio do círculo é , assim podemos esboçar o desenho a seguir:
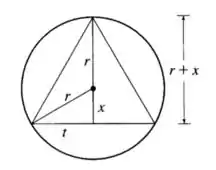
Uma das propriedades de geometria nos diz que o raio do círculo vale da altura do triângulo inscrito nele, então nessa figura, vale , e é igual a altura .
O que nós vamos fazer é definir a área desse triângulo e tentar maximizar a expressão obtida, através da derivada da função.
Então, vamos lá!
Passo 2
Primeiramente, utilizando o triângulo retângulo formado na figura, temos:
E isolamos uma das variáveis da equação:
Agora sabendo que a área do triângulo é dada pelo produto do lado com a altura, divido por , temos:
Então, substituindo e na fórmula da área, vamos ter:
Passo 3
Com a fórmula dependendo de apenas de uma variável, podemos encontrar seus pontos críticos. Primeiro derivando a equação, usando a regra do produto.
A regra do produto para derivadas é uma ferramenta usada para encontrar a derivada de um produto de duas funções.
Ela nos diz que a derivada do produto de duas funções é igual à primeira função multiplicada pela derivada da segunda, mais a segunda função multiplicada pela derivada da primeira.
Em resumo:
Isso simplifica o processo de encontrar derivadas de expressões mais complexas que envolvem produtos de funções.
E igualando esse resultado a zero:
Passo 4
Somando as frações com o mesmo denominador e simplificando:
Multiplicando os dois lados por :
Passo 5
Temos a equação do segundo grau:
Fatorando essa equação, ficamos com:
E nossas raízes serão:
E
Como não podemos obter raio negativo, obtemos nossa função tem um único ponto crítico, que ocorre quando nosso triângulo é máximo em
Passo 6
Agora encontrando as dimensões do triângulo e sua área:
Vamos ter:
E substituindo , com , temos:
Passo 7
Pra calcular a altura, vamos somar o raio e a distância :
Substituindo :
E temos as dimensões do triângulo que maximizam a nossa área.
Valeu, galera! Até a próxima! 😉
“Às vezes é preciso aprender a correr antes de começar a andar”
