Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.2 - Ex. 44
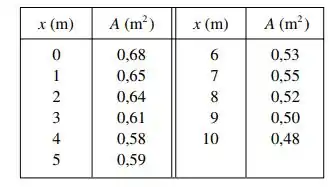
Um tronco de de comprimento é cortado a intervalos de e as suas áreas de secção transversal (a uma distância da extremidade do tronco) estão listadas na tabela. Use a Regra do Ponto Médio com para estimar o volume do tronco.
Passo 1
Com nosso variando de a temos o seguinte delta:
Nossos pontos extremos são e , logo, nossos pontos médios são e .
Passo 2
Assim, a fórmula do nosso volume é:
Resposta
Exercícios de Livros Relacionados
Use a) a regra do trapézio, b) a regra do ponto médio, e c) a regra de Simpson para aproximar a a integral dada com os valores dados de n . (Aproxime sua resposta para seis casas decimais.)
Use a) a regra do trapézio, b) a regra do ponto médio, e c) a regra de Simpson para aproximar a a integral dada com os valores dados de n . (Aproxime sua resposta para seis casas decimais.)
Use a) a regra do trapézio, b) a regra do ponto médio, e c) a regra de Simpson para aproximar a a integral dada com os valores dados de n . (Aproxime sua resposta para seis casas decimais.)
A região delimitada pela curva y = 1 / ( 1 + e - x ) , os eixos x e y , e a linha x = 10 é rotacionada em torno do eixo x . Use a regra de Simpson com n = 10 para estimar o volume do sólido resultante
Use a) a regra do trapézio, b) a regra do ponto médio, e c) a regra de Simpson para aproximar a a integral dada com os valores dados de n . (Aproxime sua resposta para seis casas decimais.)