Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.3 - Ex. 21
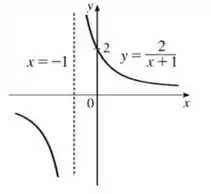
Faça o gráfico de cada função, sem marcar pontos, mas começando com o gráfico de uma das funções básicas dadas na Seção e então aplicando as transformações apropriadas.
Passo 1
E aí galera, tudo bem? Vamos fazer aqui mais uma questão sobre transformação de funções e gráficos. No livro do Stewart, na Seção , nos é dado essa gráfico:
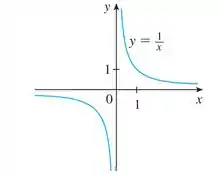
Que é o gráfico da função recíproca , ta ok? Esse gráfico é importante e aparece com certa frequência em Cálculo, então fica a dica, é daqueles que você tem que saber de cabeça!
A primeira coisa que vamos fazer é deslocar o gráfico na horizontal em unidade para a esquerda. Os deslocamentos na horizontal sempre vão acontecer quando somamos ou subtraímos um número bem do lado do , fechou? Olha como vai ficar:
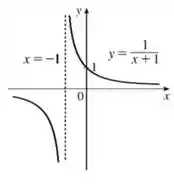
Passo 2
Agora temos que esticar o nosso gráfico na vertical por um fator . Lembr-se que, sempre quando multiplicamos toda a expressão por um número ou dividimos, nosso gráfico vai ficar mais deformado na vertical, belê? Olha como fica:
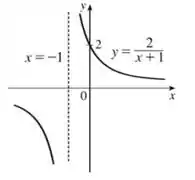
Pronto! Esse já é o nosso gráfico de !
Resposta
O gráfico de é:
