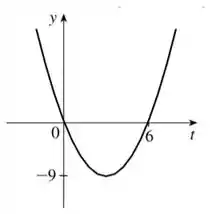
Encontre o domínio e esboce o gráfico da função:
Passo 1
E aí galera, beleza?
Veja bem, aqui temos que resolver essa atividade que nos pede para encontrarmos o domínio e esboçarmos o gráfico da função.
O domínio nada mais é do que o conjunto de valores de possíveis de serem utilizados pela nossa função. Algumas funções possuem restrições, como por exemplo não podermos dividir por zero.
Bom, aqui temos uma função polinomial do segundo grau, sem nenhum tipo de radical e sem nenhuma variável no denominador da função.
Passo 2
Toda vez que a gente tiver um polinômio de qualquer grau que atenda essas condições, seu domínio será todos os números reais, ou seja o conjunto .
Só mais uma coisinha, antes que a gente esqueça: vamos chamar de , combinado? Vamos adiante!
Como a gente tem uma função do segundo grau, seu gráfico vai ser uma parábola! Essa é daquelas funções que tão sempre aparecendo durante os exercícios de cálculo, então incorpora o Bháskara e não esquece dela!
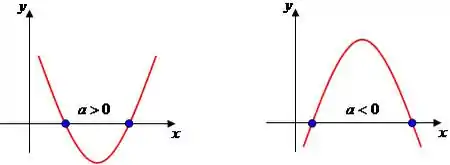
A primeira dica é aquela de sempre olhar o sinal que acompanha o termo ao quadrado. Se for positivo, a concavidade da parábola tá virada pra cima, se for negativo, a concavidade da parábola tá virada para baixo.
Como aqui a gente tem e não , nos sabemos que nossa concavidade ta pra cima!
Temos que achar pontos para montar a nossa parábola no plano cartesiano. Primeiro, iremos encontrar as raízes do nosso polinômio, isto é, resolver a equação:
Pra resolver essa a gente pode deixar o em evidência, ficando assim:
Isso vai ser verdade quando ou ou . Do segundo caso, tiramos que . Pronto! Agora temos dois pontos, sendo eles, na forma de um par ordenado , os pontos e .
Passo 3
Para achar o terceiro ponto, podemos achar os dois que já temos. É só a gente pegar os valores que encontramos, somar e dividir por dois. Isso vais nos levar exatamente para o meio da parábola, que é onde temos o seu ponto de menor valor, ajudando bastante na hora de desenhar o gráfico! Esse ponto vai ser onde vamos ter um :
Substituindo em nossa expressão, vamos encontrar:
Logo, o nosso último ponto vai ser o par ordenado .
Passo 4
Agora, de posse dos pontos, , e , podemos desenhar nosso gráfico! Lembra que o último ponto representa o ponto mais baixo da parábola, valeu? Olha só como vai ficar:
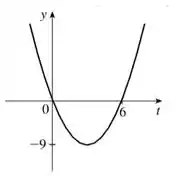
Resposta
O domínio da função é o conjunto dos números reais e seu gráfico é dado por: