Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 35
Encontre o domínio da função
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente encontre o domínio da seguinte função:
Mas o que é esse domínio??
Bom... Determinar o domínio da função é o mesmo que dizer quais valores de podemos por na função sem que haja nenhum problema. Ou seja, são os valores de para os quais a nossa função está definida.
A gente tem sempre que lembrar que para funções definidas por um quociente, seu denominador nunca pode ser zero. Além disso, quando temos uma raiz de índice par, seu radicando nunca pode ser negativo. Então, vamos trabalhar com essas retrições.
Vamos lá!
Passo 2
Vamos analisar nossa função para achar onde podemos ter algum problema:
Bom, temos uma divisão e ela não pode ter o denominador igual zero, e temos uma raiz de índice par que não pode ser negativa.
Então, nesse caso, o termo que está dentro da raiz precisa ser apenas maior do que zero, ou seja:
Podemos colocar em evidência:
Para que essa multiplicação seja um número positivo, os dois termos precisam ser positivos ou os dois termos precisam ser negativos.
Assim, para que os dois termos sejam positivos, temos:
E
E para que os dois termos sejam negativos, temos:
E
Passo 3
Vamos analisar agora:
Para e :
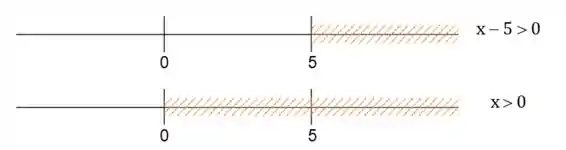
Podemos ver que , possui parte de , pegando só a interseção dos dois, temos:
Agora para e :
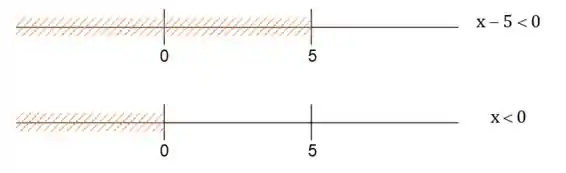
Também, podemos ver que , possui parte em , então a interseção dos dois conjuntos vai nos dá:
Agora vamos escrever nosso domínio, ele será a união das duas análises para maiores que zero e menores que zero, então:
Arrasamos!!!!!!
Valeu, galera! Até a próxima! 😉