Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 4h
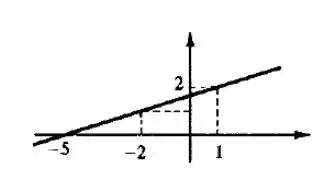
Dê o domínio e esboce o gráfico.
Passo 1
Oi pessoal, tudo bem? Vamos começar essa questão achando o domínio!
Para esboçar o domínio precisamos pensar se essa função tem alguma restrição para o valor de . Entre as restrições temos:
- O denominador em uma fração não pode ser zero
- O argumento de uma raiz par não pode ser menor que zero
- O argumento de uma função logarítmica não pode ser negativo
Note que embora tenhamos uma fração na nossa função, não tem como o denominador zerar, pois o está multiplicando. Logo, não temos nenhuma restrição e o domínio serão todos os reais.
Agora que já sabemos o domínio, vamos pra o esboço do gráfico!
Passo 2
Temos aqui um polinômio de grau um, ou seja, esse gráfico é uma reta. Então vamos determinar dois pontos dessa equação e traçar a reta.
Vamos escolher os pontos e .
Para o ponto , temos
Então temos um ponto
Agora para ,
Então corta no ponto
Passo 3
Agora é só colocar num gráfico:
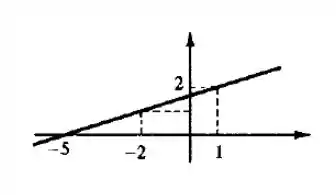
Resposta
Exercícios de Livros Relacionados
Dê o domínio e esboce o gráfico.g ) g (x) = - 2
Dê o domínio e esboce o gráfico.c ) h (x) = - x + 1
Dê o domínio e esboce o gráfico.i ) f (x) = - (1)/(2) x
Dê o domínio e esboce o gráfico.j ) g (x) = {[[x , s e x = 2],[3 , s e x2]])