Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 40
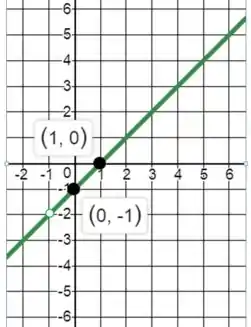
Encontre o domínio e esboce o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte função:
Queremos encontrar o domínio e o esboço do gráfico dessa função.
Para isso, temos que entender alguns conceitos:
- O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função é definida;
- A imagem de uma função é o conjunto de todos os valores de saída que a função pode produzir quando aplicada aos elementos do domínio.
Assim, para resolver essa questão, a primeira coisa que devemos encontrar é o domínio da função!! Ou seja, quais os valores possíveis de , que a nossa função é definida.
De forma mais simples, para encontrar o domínio, podemos ver se existe algum valor de para qual a função dá problema.
Dar problema pode ser por exemplo um denominador ser zero, uma raiz quadrada ser negativa, etc...
No caso da função mostrada, a única restrição é o denominador não ser zero.
E aí?? Bora lá?? 😉
Passo 2
Portanto, como não queremos dividir por zero, temos queÇ
Logo,
Assim o domínio são todos os números reais com , ou seja:
Passo 3
Beleza, agora podemos modificar esta função para ficar mais fácil esboçar o gráfico. Veja o numerador da função:
Logo:
Aqui podemos cortar com , mas essa divisão só é possível, pois estamos considerando que não pode ser , se não a gente poderia ter uma divisão por .
Por ser uma equação do primeiro grau, temos uma reta.
Assim, bastam pontos para definir como será o gráfico.
Vamos então aos pontos quando
, e quando :
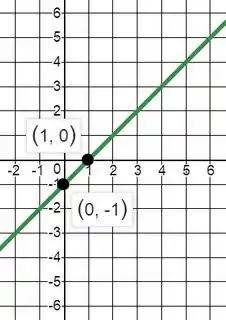
Mas temos que tomar um cuidado aqui!! A nossas função não é definida para , logo, temos que tirar esse ponto do nosso gráfico.
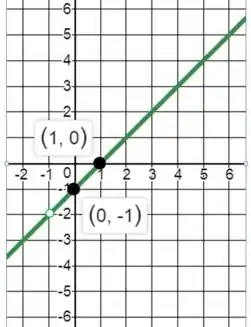
Resposta
