A família de funções , onde , e são números positivos e , tem sido usada para modelar a concentração de uma droga injetada na corrente sanguínea no instante . Faça o gráfico de vários membros dessa família. O que eles têm em comum? Para valores fixos de e , descubra graficamente o que acontece à medida que cresce. Use então o cálculo para demonstrar o que você descobriu.

Vamos usar Python para gerar esses gráficos e explorar o comportamento da função.

Em seguida, usaremos cálculo para demonstrar analiticamente o que observamos nos gráficos.

import numpy as np

import matplotlib.pyplot as plt

# Definir os valores de C e a fixos

C = 1

a = 1

# Definir os valores de b variáveis

b_values = [2, 3, 4]

# Definir o intervalo de tempo

t = np.linspace(0, 5, 400)

# Plotar as funções para diferentes valores de b

plt.figure(figsize=(10, 6))

for b in b_values:

f = C * (np.exp(-a * t) - np.exp(-b * t))

plt.plot(t, f, label=f'b = {b}')

# Configurações do gráfico

plt.title('Família de funções f(t) = C (e^{-at} - e^{-bt}) para C = 1, a = 1 e diferentes valores de b')

plt.xlabel('t')

plt.ylabel('f(t)')

plt.legend()

plt.grid(True)

plt.show()

Primeiro, vamos traçar os gráficos para valores fixos de e variar

- Fixaremos

- Variamos entre

Vamos plotar essas funções.

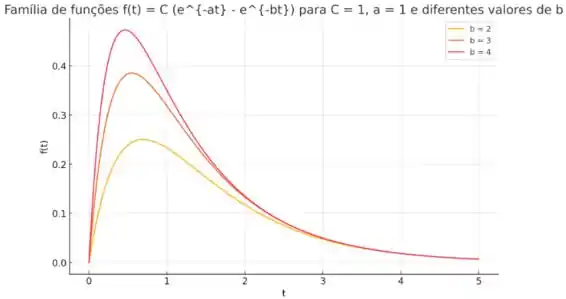
Os gráficos mostram que, para valores fixos de e diferentes valores de , as funções

Compartilham algumas características comuns:

1. Ponto inicial: Todas as funções começam no ponto com valor

2. Comportamento inicial: No início, cresce rapidamente à medida que aumenta a partir de zero.

3. Pico e Decaimento: Todas as funções atingem um pico e depois decaem para zero conforme aumenta, mas o tempo em que atingem o pico e a forma do decaimento variam com

Agora, vamos analisar graficamente o que acontece à medida que cresce, mantendo fixos.

Podemos observar que:

- À medida que aumenta, o pico da função ocorre mais rapidamente e a função retorna a zero mais rapidamente.

Vamos usar cálculo para demonstrar analiticamente o comportamento observado.

A função é dada por:

Para entender o comportamento da função à medida que cresce, precisamos encontrar os pontos críticos, onde a derivada da função é zero.

A primeira derivada de é:

Encontramos os pontos críticos resolvendo

Vamos resolver essa equação para

Os pontos críticos da função ocorrem em:

Como são constantes positivas e este ponto é bem definido.

Vamos analisar o comportamento desse ponto crítico:

1. Posição do Pico: O ponto

Representa o tempo em que a concentração da droga atinge seu valor máximo.

2. Dependência de À medida que aumenta, o valor de para o pico diminui. Isso é consistente com a observação de que o pico ocorre mais cedo para valores maiores de

Para , vamos expressar explicitamente o ponto crítico em termos de

Vamos usar Python para gerar esses gráficos e explorar o comportamento da função.

from sympy import symbols, Eq, solve, exp

# Definir as variáveis

t, a, b, C = symbols('t a b C', real=True, positive=True)

# Definir a função e sua derivada

f = C * (exp(-a*t) - exp(-b*t))

f_prime = f.diff(t)

# Resolver f'(t) = 0 para t

critical_points = solve(Eq(f_prime, 0), t)

critical_points

Podemos traçar um gráfico desse ponto crítico em função de para visualizar essa dependência.

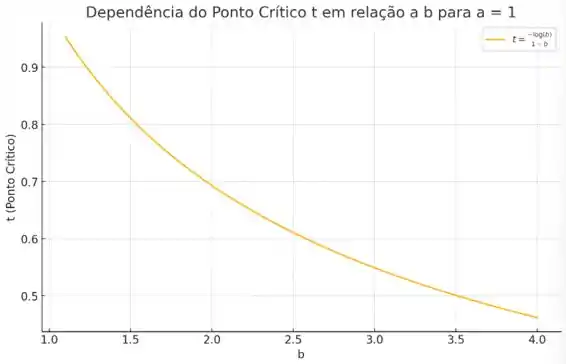
O gráfico mostra que, à medida que aumenta, o tempo em que a função atinge seu pico diminui.

Isso confirma a observação de que o pico ocorre mais cedo para valores maiores de

1. Comportamento Comum: Todas as funções da família

têm um comportamento similar: começam em zero, aumentam rapidamente, atingem um pico e depois decaem para zero.

2. Efeito de : Para valores fixos de , à medida que aumenta:

- O pico da função ocorre mais cedo.

- A função retorna a zero mais rapidamente.

3. Análise Analítica: A análise da derivada mostrou que o ponto crítico ocorre em

que diminui à medida queaumenta, confirmando as observações gráficas.

Essa combinação de análise gráfica e cálculo fornece uma compreensão completa do comportamento da família de funções e como os parâmetros afetam essa dinâmica.

# Definir valores de b

b_vals = np.linspace(1.1, 4, 400) # Evitar b = 1 para prevenir divisão por zero

# Calcular pontos críticos t para a = 1

a_val = 1

t_critical = -np.log(b_vals) / (a_val - b_vals)

# Plotar o ponto crítico em função de b

plt.figure(figsize=(10, 6))

plt.plot(b_vals, t_critical, label=r'$t = \frac{-\log(b)}{1 - b}$')

plt.xlabel('b')

plt.ylabel('t (Ponto Crítico)')

plt.title('Dependência do Ponto Crítico t em relação a b para a = 1')

plt.grid(True)

plt.legend()

plt.show()