Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 42
Encontre uma equação para a cônica que satisfaça as condições dadas:
Elipse, focos , passando por
Passo 1
Fala ai! Partiu resolver uma questãozinha juntos?
1- Vamos identificar o centro da Elipse.
2- Calcular a distância entre os Focos.
3- Vamos usar a equação fundamental da Elipse, substituindo todos os termos.
Pegou a visão? Vamos então começar!
Passo 2
Por ter focos em conseguimos tirar todas as informações importantes dessa elipse, conseguimos dizer que a elipse tem centro na origem, que a elipse tem eixo maior na horizontal e que tem valor de .
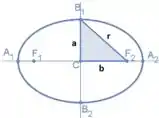
Sendo assim, vamos usar a equação dê:
Passo 3
Utilizamos o teorema de Pitágoras
Já que para a termos um eixo maior na horizontal o valor de nessa equação deverá ser a maior.
Passo 4
Já que a elipse passa por , substituindo o ponto em e , teremos a seguinte equação:
Onde:
Resolvendo o MMC do lado esquerdo da equação
Substituindo , nós teremos:
Passo 5
Para e Resolvemos a equação de Bhaskara para encontrarmos as raízes.
Porém então não podemos ter valores negativos de logo:
E substituindo em , temos
Logo a equação da elipse ficará da seguinte forma: