Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 13

Encontre os vértices e os focos da elipse e esboce seu gráfico.

4 x 2 + y 2 = 16

Passo 1

Fala ai galerinha. De boa? O objetivo dessa questão é encontrar os vértices e os focos de uma elipse dada pela equação 4 x ² + y ² = 16 e esboçar seu gráfico. Como podemos resolver?

  1. Reescrever a equação na forma padrão da elipse.

    2. x 2 a 2 + y 2 b 2 = 1

    Em que a é o semieixo em x e b é o semieixo em y .

  2. Identificar os parâmetros e os vértices.
  3. Calcular os focos ( c ) , com a equação

    4. c = a 2 + b 2

  4. Esboçar o gráfico.

Bora resolver!

Passo 2

Como só temos um termo x 2 e outro y 2 então já podemos dizer que temos uma elipse centrada na origem e a equação da elipse centrada na origem tem a seguinte equação característica.

x 2 a 2 + y 2 b 2 = 1

A equação dada foi:

4 x 2 + y 2 = 16

Então teremos que transformar a equação até ficar com essa cara da elipse. A primeira ação é passar o 16 dividindo.

4 x 2 16 + y 2 16 = 1

Simplificando o termo de x . Temos

x 2 4 + y 2 16 = 1

Passo 3

Comparando as duas equações temos que descobrir o valor de a e o valor de b .

x 2 a 2 + y 2 b 2                       →                         x 2 4 + y 2 16

Para a

a 2 = 4

a 2 = 4

a = ± 2

e

b 2 = 1 6

b 2 = 16

b = ± 4

O que nos diz que o eixo maior está no eixo y , já que b > a . Além de que teremos vértices em

( ± 2,0 )

e

( 0 , ± 4 )

Passo 4

Como b > a teremos os focos também no eixo vertical e eles estarão na posição de:

( 0 , ± c )

Onde c valerá:

c = b 2 - a 2

c = 4 2 - 2 2

c = ± 12

c = ± 2 ∙ 2 ∙ 3

c = ± 2 ² ∙ 3

O foco da elipse será:

c = ± 2 3

Passo 5

Para construir o gráfico devemos levar em consideração os seguintes termos calculados

a = ± 2 b = ± 4 c = ± 2 3

Obtemos o seguinte gráfico

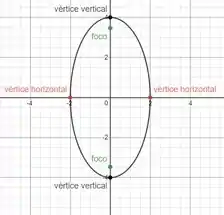
Resposta

Vértices horizontais:

± 2,0

Vértices verticais:

( 0 , ± 4 )

Foco:

( 0 , ± 2 3 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache uma equação da circunferência satisfazendo as condições dadas: Tangente à reta 3 ⋅ x + 4 ⋅ y - 16 = 0 em 4 ,1 e com um raio de 5 (duas circunferências possíveis).
Ache uma equação da circunferência satisfazendo as condições dadas: Tangente à reta 3 ⋅ x + y + 2 = 0 em - 1 ,1 e passa pelo ponto 3 ,5 .
Ache uma equação de cada uma das duas retas com inclinação - 4 3 , que são tangentes à circunferência x 2 + y 2 + 2 ⋅ x - 8 ⋅ y - 8 = 0 .
Prove que um gráfico que seja simétrico com respeito a ambos os eixos coordenados também seja simétrico com respeito à origem.
O gráfico de uma equação em x e y será simétrico com respeito à reta y = x se e somente se está for equivalente à equação obtida quando x for substituído por y e y por x. Mostre que o gráfico da equaç