Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 13
11-16. Encontre os vértices e os focos da elipse e esboce seu gráfico.
13.
Passo 1
Nessa questão, nos foi dada a equação de uma elipse, para encontrarmos seus vértices e focos. A equação é dada por
Podemos reescrever (dividindo a equação toda por 16) como
Observe que como não temos nenhum número somando ou subtraindo do e do podemos dizer que a elipse é centrada na origem.
A equação geral de uma elipse centrada na origem é , e quando temos o número maior embaixo do esta é uma elipse com eixo maior no eixo .
O foco dessa elipse (caso ) é dado por
O vértice dessa elipse (caso ) é dado por
Para resolver a questão vamos encontrar os valores apresentados na equação para em seguida substituir na relação que nos dá a posição dos focos e vértices.
Passo 2
Em primeiro lugar vamos encontrar os valores a partir da equação apresentada. A equação da elipse dada pelo problema é dada por
Comparando à equação da elipse
Chegamos aos resultados
Passo 3
Encontrados os valores de podemos substituí-los na equação que nos diz as coordenadas dos focos e dos vértices.
Os vértices de uma elipse centradas na origem são:
Então,
Passo 4
Como apresentado no passo 1, temos que na equação apresentada o maior número está dividindo a variável , o que significa que nossa elipse possui maior distância entre seus extremos nesse eixo.
Para esboçar a elipse precisamos marcar no gráfico 4 pontos: .
Esses pontos representam as extremidades da elipse. Além desses pontos, precisamos marcar os pontos de foco e de vértices .
Vamos esboçar essa elipse baseado em nossas considerações e valores encontrados:
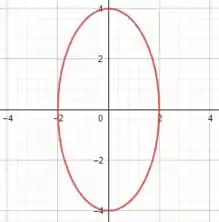
Resposta
