Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 42
Encontre a equação para a cônica que satisfaz as condições dadas
Passo 1
Aoba meus queridos, tudo bom? Nessa questão a gente precisa montar uma equação que descreva uma elipse com focos e que passe especificamente pelo ponto . Para dar um norte, vamos tentar desenhar um esboço dessa elipse com esses dados:
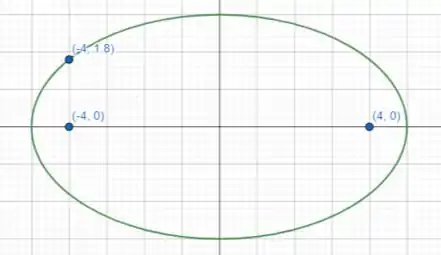
Note que essa é uma elipse com eixo maior no eixo , podemos ver isso pelas coordenadas do foco, que mudam apenas em .
A gente sabe (e se não sabe vai aprender agora) que elipses tem equações no formato:
Só precisamos identificar essas variáveis e substituir na equação geral!
Passo 2
O par é o centro da elipse, e sabemos que o centro da elipse fica na metade do caminho entre seus focos. Então, como aqui temos , nosso centro será . Portanto
Além disso:
é a distância do centro da elipse até um dos vértices, que ainda não sabemos
é a distância do centro da elipse até um dos “vértices” do eixo menor, que também não sabemos
E por fim, é a distância do centro da elipse ao foco, então teremos
Para matar a charada de vez, sabemos ainda que existe uma relação entre , tal que
Substituindo o valor que temos:
Vamos guardar essa informação por enquanto.
Enquanto isso, vamos substituir o ponto na equação geral da elipse:
Substituindo o valor de que encontramos antes nessa nova equação, temos:
Observe que chegamos em uma equação do segundo grau em que a variável é :
E se fizermos
Temos:
Uma vez que encontrarmos será fácil encontrar e então substituir na fórmula geral.
Passo 3
Resolvendo essa equação de segundo grau:
Esse resultado vai ser descartado pois
Assim:
Agora, podemos determinar o valor de !
E, finalmente, podemos escrever a equação da cônica!