Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 27
Encontre equações paramétricas e um intervalo de parâmetro para o movimento de uma partícula que começa no ponto e traça a metade superior do círculo quatro vezes.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
No início da tarefa, notamos que a equação dada é a equação do círculo com centro na origem e raio .
Como a partícula se move na parte superior do círculo, desenharemos apenas a parte do círculo que está acima do eixo .
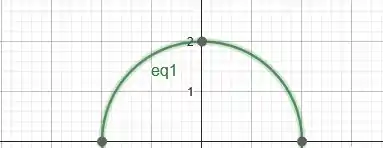
A equação do círculo é dada por
na notação de parâmetro, escrevemos como
Ou seja, de acordo com a identidade trigonométrica pitagórica a relação entre seno e cosseno é dada pela seguinte expressão:
Portanto, a equação de todo o círculo na equação paramétrica usando a notação (1) e (2) é:
Passo 2
Sabemos que a partícula começa no ponto . É quando o ângulo é igual a (o parâmetro é ). Como a partícula se move apenas na parte do círculo acima do eixo x, o ângulo t assume valores de a . Devido ao período das funções seno e cosseno, t assume valores
Pelas condições da tarefa, sabemos que a partícula se move 4 vezes ao longo da parte superior do círculo, portanto, t assume os valores:
O círculo está acima do eixo x, então y é sempre positivo. Para que o ângulo t sempre retorne um valor de seno positivo, escreveremos y como um valor absoluto:
Por causa do valor absoluto, quando t assume valores de π a 2π, todos os valores no círculo abaixo do eixo x serão mapeados para valores acima do eixo x.
Em outras palavras, quando t assume valores de π a 2π, devido ao valor absoluto, a partícula se move na parte do círculo acima do eixo x de modo que ela se mova no sentido horário (do ponto (−2,0) a (2,0)).