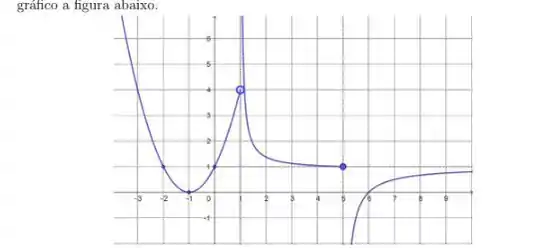
Exercícios de Introdução às Curvas e Domínio de Curvas - Lista de Exercícios Resolvida
Questão 2
Um projétil é lançado de uma altura com uma velocidade , como ilustrado pela figura a seguir:
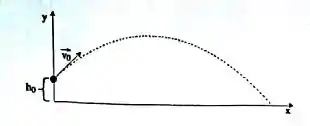
Sabendo que esse projétil está submetido à aceleração da gravidade (, a sua trajetória pode ser parametrizada da seguinte maneira:
Questão 3
Para a função com fórmula
a) Determine o domínio máximo dessa função.
b) Esboce as curvas de nível , e para essa função no mesmo plano.
c) Existe um ponto (a,b) no qual essas 3 curvas de nível parece se encontrar. Encontre esse ponto e explique como é possível.
Ver solução completaQuestão 12
5. Encontre uma fórmula para a função descrita e obtenha seu domínio.
b) Uma caixa retangular aberta com volume de tem uma base quadrada. Expresse a área da superfície da caixa como uma função do comprimento de um lado da base.
Ver solução completaQuestão 13
5. Encontre uma fórmula para a função descrita e obtenha seu domínio.
a) Expresse a área de um triângulo equilátero como uma função do comprimento de um lado
Ver solução completaQuestão 18
Seja a função, e o conjunto
Resolva as questões,
a seguir trace um esboço mostrando como um sólido sombreado em , o conjunto de pontos do domínio de .
Ver solução completaQuestão 21
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 22
Calcular o limite dado, usando teoremas de limites ou álgebra de limites.
c)
Ver solução completaQuestão 25
5. Encontre uma fórmula para a função descrita e obtenha seu domínio.
c) Uma caixa sem tampa deve ser construída de um pedaço retangular de papelão com dimensões por . Para isso, devem-se cortar quadrados de lados de cada canto e depois dobrar, conforme mostra a figura. Expresse o volume da caixa como uma função de .
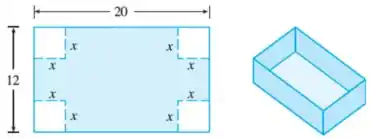
Questão 27
Em cada caso esboce alguma curvas de nível da função , de modo a obter uma visualização do seu gráfico.
Ver solução completaQuestão 28
Em cada caso identifique e represente graficamente o domínio da função .
Ver solução completaQuestão 29
Em cada caso identifique e represente graficamente o domínio da função .
Ver solução completaQuestão 30
Em cada caso identifique e represente graficamente o domínio da função .
Ver solução completaQuestão 31
Em cada caso identifique e represente graficamente o domínio da função .
Ver solução completaQuestão 32
Em cada caso identifique e represente graficamente o domínio da função .
Ver solução completaQuestão 34
(Capítulo 13.1 – Exercício 14) Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce.
Ver solução completaQuestão 51
Considere as curvas
Dadas as superfícies
É correto afirmar que:
- A imagem de está contida em e a imagem de está contida em
- A imagem de está contida em e a imagem de está contida em
- A imagem de está contida em e a imagem de está contida em
- A imagem de está contida em e a imagem de está contida em
Questão 52
Ao criar uma função (ou definir uma função, usando o linguajar matemático), devemos especificar o domínio, o contradomínio e a regra de formação (ou regra de associação) da função. Por exemplo, dada por tem domínio , contradomínio e regra de formação . Porém, nem sempre essas três informações fornecem uma função. Por exemplo dada por não é uma função, pois a regra não pode ser aplicada a todos os elementos do domínio. Neste
caso, dizemos que não está bem definida (caso fosse uma função, diríamos que está bem definida).
Em cada um dos itens abaixo, diga quais estão ou não bem definidos.
a) dada por
b) dada por
c) dada por
d) dada por
e) dada por
f) dada por é o número cujo quadrado é .
Ver solução completaQuestão 53
Normalmente, o caminho para se definir uma função é escolher o domínio, o contradomínio e, por fim, a regra de formação. Porém, em certas situações, a regra de formação é escolhida inicialmente. Nesse caso, fica a pergunta de que escolhas podemos fazer para o domínio e o contradomínio de forma que se obtenha uma função bem definida. Por exemplo, para a regra de formação podemos escolher como domínio e como contradomínio. Obviamente, há infinitas escolhas que funcionam nesse caso. Convencionou-se, nos cursos de Cálculo que, quando uma regra de formação é fornecida (sem domínio e contradomínio), o domínio é o maior subconjunto de de forma que a regra de formação possa ser calculada dentro do conjunto dos números reais e que o resultado também seja um número real. Por exemplo, o maior subconjunto de para o qual a expressão pode ser calculada usando número reais é . Com isso, dizemos que o domínio da função é . Em cada um dos itens abaixo, encontre o domínio das funções, conforme exemplos nos itens (a) e (b).
Observação. Não há uma convenção absoluta para o contradomínio quando este não é especificado. As duas convenções mais usadas são usar ou usar o conjunto imagem como contradomínio.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 54
Diga quais dos conjuntos abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 55
Seja uma função inversível (isto é, que possui inversa) e suponha que e que . Determine e .
Ver solução completaQuestão 56
Faça o gráfico das funções abaixo, encontrando alguns dos pontos pertencentes ao gráfico e tentando deduzir o restante. O objetivo aqui é mostrar que existe uma forma de fazer o gráfico de qualquer função, basta encontrarmos diversos pontos pertencentes ao seu gráfico. Obviamente, esse método é entediante, mas é importante utilizá-lo uma vez na vida. Ao longo desse curso, aprenderemos técnicas para encontrar o gráfico de certas funções sem precisar recorrer ao método desse exercício. Futuramente, em Cálculo , você aprenderá mais técnicas para traçar o gráfico de funções.
a) dada por
b) dada por
c) dada por
d) dada por
Ver solução completaQuestão 57
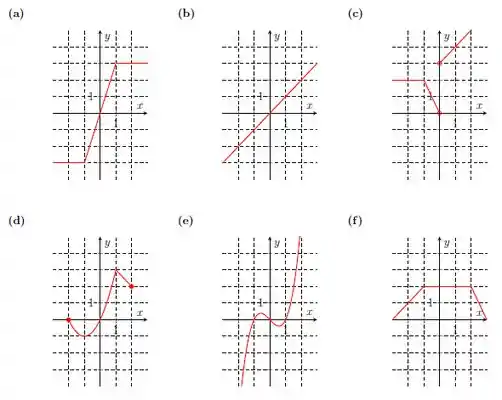
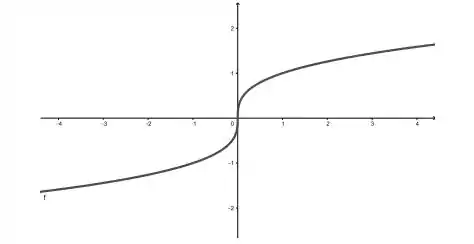
Sejam uma função e um intervalo contido no domínio de . Dizemos que é crescente em se para quaisquer e com . Em outras palavras, o valor de aumenta à medida que aumenta. Similarmente dizemos que é decrescente em se para quaisquer e com . Quando dizemos que é crescente (sem mencionar intervalo), significa que é crescente em todo seu domínio (o mesmo se aplica para decrescente). Por exemplo, considere a função cujo gráfico é dado pela figura abaixo.
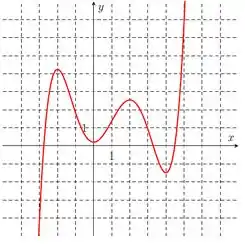
Note que a função é crescente em , em e em e é decrescente em e em . Nos itens abaixo, diga os intervalos de crescimento e decrescimento das funções.
Questão 58
Em cada um dos itens abaixo calcule o que se pede.
a) dada por . Calcule .
b) dada por . Calcule .
Ver solução completaQuestão 59
Faça o gráfico das funções abaixo (a partir daqui, você pode usar seus conhecimentos sobre funções para fazer o gráfico):
a)
b)
Ver solução completaQuestão 60
Diga quais dos gráficos abaixo representam uma função com domínio e contradomínio . Nos casos que são funções, determine o conjunto imagem.
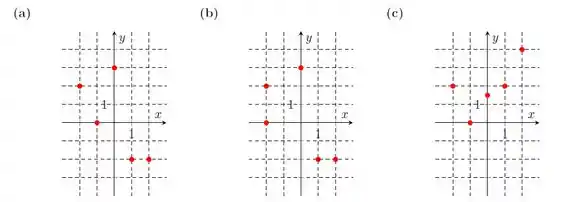
Questão 61
Sempre que uma função não está bem definida (conforme exercício anterior), podemos fazer certas alterações para a tornar bem definida. Há, basicamente, três formas de fazer isso: (A) restringir o domínio, (B) aumentar o contradomínio ou (C) modificar a regra de formação. Para cada um dos itens do exercício anterior que não estão bem definidos, corrija a definição utilizando um dos três métodos acima, conforma no exemplo do item (a).
Ver solução completaQuestão 62
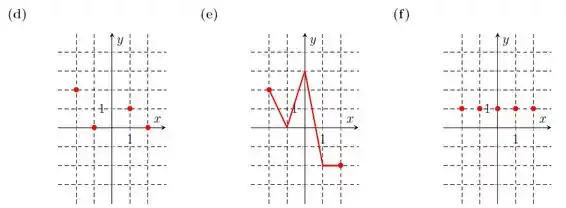
Diga quais dos gráficos abaixo representam alguma função. Nos casos que são funções, determine o domínio.
Questão 64
A função é definida como
Calcule e
Qual é o domínio desta função?
Verifique que esta função é par.
Faça o gráfico. Sugestão. Faça o gráfico de e e utilize a adição de gráficos.
Ver solução completaQuestão 66
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 67
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 72
Faça o gráfico e encontre o conjunto imagem das funções abaixo.
a)
b)
c)
d)
Ver solução completaQuestão 73
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 74
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 75
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 76
Encontre o domínio e a imagem da função e trace um esboço mostrando uma região sombreada em , como um conjunto de pontos no domínio de .
Ver solução completaQuestão 77
Os gráficos abaixo representam funções. Determine o domínio e a imagem de cada uma delas.
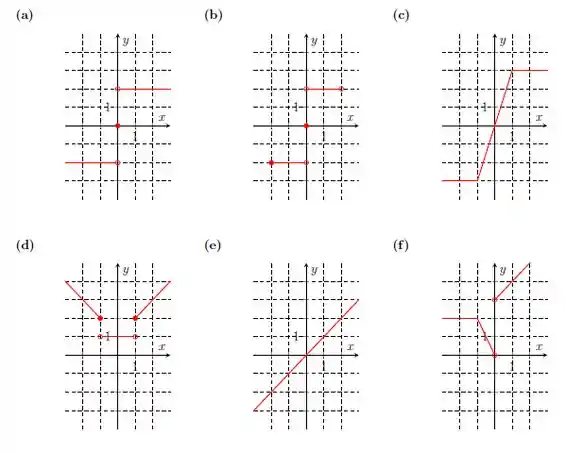
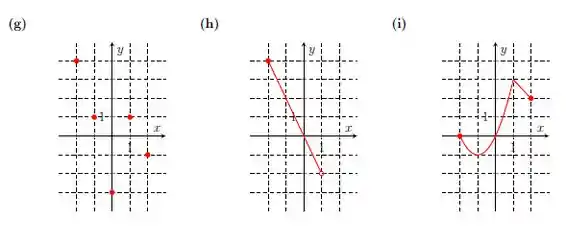
Questão 82
Suponha que seja encontrado a partir da fórmula , onde seja determinando que e sejam e com erros máximos possíveis de . Calcule o erro máximo possível no valor computado de .
Ver solução completaQuestão 83
Encontre o domínio, a imagem e esboce o gráfico do domínio da função:
Ver solução completaQuestão 84
(Capítulo 13.1 – Exercício 7) Esboce o gráfico da curva cuja equação vetorial é dada. Indique
com setas a direção na qual o parâmetro t cresce.
Ver solução completaQuestão 85
(Capítulo 13.1 – Exercício 9) Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce.
Ver solução completaQuestão 86
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
b)
Ver solução completaQuestão 87
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
c)
Ver solução completaQuestão 88
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
d)
Ver solução completaQuestão 90
Seja . Determine o domínio de , os valores de onde a se anula e os intervalos onde a é positiva e onde a é negativa.
Ver solução completaQuestão 91
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
g)
Ver solução completaQuestão 92
8. Determine o domínio e execute as operações indicada nas expressões abaixo. Em seguida, simplifique essas expressões, fatorando numerador e o denominador, caso necessário.
(b) .
Ver solução completaQuestão 93
1. Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.
(a) ; .
Ver solução completaQuestão 95
1. Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.
(b) ; .
Ver solução completaQuestão 97
20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
b)
Ver solução completaQuestão 98
21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
b) e .
Ver solução completaQuestão 99
21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
c) e .
Ver solução completaQuestão 100
20. Para cada uma das funções abaixo, determine o domínio, calcule (se pertencer ao domínio), faça o gráfico e determine o conjunto imagem.
c)
Ver solução completaQuestão 101
21. Para as funções e abaixo, determine as funções , , , e e encontre seus domínios.
a) e .
Ver solução completaQuestão 102
9. Usando o conhecimento do gráfico da função potência , para um inteiro , produtos notáveis e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(i) .
Ver solução completaQuestão 103
Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:
Ver solução completaQuestão 104
Caso existam, defina as funções , , e nos casos dados a seguir. Em cada caso, determine o domínio da função resultante.
; .
Ver solução completaQuestão 105
Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:
Ver solução completaQuestão 106
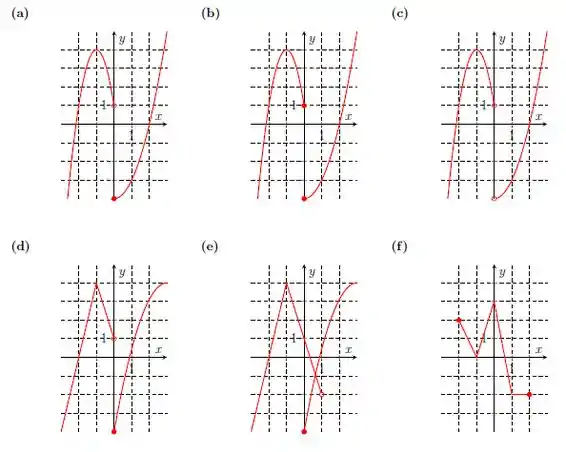
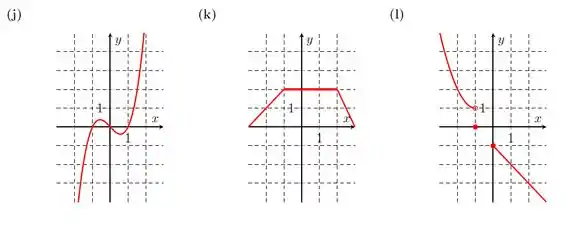
Considere a função cujo gráfico é dado a seguir e faça o que se pede
Determine o domínio e a imagem da função inversa de ;
Ver solução completaQuestão 107
Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:
Ver solução completaQuestão 108
8. Determine o domínio e execute as operações indicada nas expressões abaixo. Em seguida, simplifique essas expressões, fatorando numerador e o denominador, caso necessário.
(a) .
Ver solução completaQuestão 109
9. Usando o conhecimento do gráfico da função potência , para um inteiro , produtos notáveis e as noções de deslocamento horizontal e vertical, trace um esboço do gráfico das seguintes funções:
(ii) .
Ver solução completaQuestão 110
Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:
Ver solução completaQuestão 113
1.4) Escreva como função das variáveis e esboce o gráfico da função
a)
b)
c)
d)
Ver solução completaQuestão 114
1.1) Seja
a) Calcule e
b) Determine e esboce o domínio de .
c) Determine a imagem de .
Ver solução completaQuestão 118
Encontre uma restrição para cada função dada de modo que essa restrição admita uma inversa . Em cada caso, especifique o domínio e o contradomínio da inversa, e também, sua lei de formação, nos casos seguintes:
Ver solução completaQuestão 119
Encontre o domínio da função . Encontre as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados.
Esboce o gráfico de . Explique a construção do gráfico da função ,
usando transformações em gráfico (translações, reflexões...) a partir do gráfico da função .
Descreva essas transformações em palavras.
Ver solução completaQuestão 120
Esboce a região da integração e mude a ordem de integração para calcular a integral:
Ver solução completaQuestão 138
Um papel de filtro circular de raio a deve ser transformado em um filtro cônico cortando um
setor circular e juntando as arestas CA e CB (veja a Figura 3a). Ache a razão entre o raio e a
profundidade do filtro de capacidade máxima.
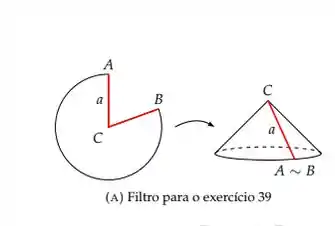
Questão 139
- Dada a função definida por
- Trace o gráfico de e determine o e
- Discuta a continuidade de nos números , e .
Questão 140
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 141
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 142
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 143
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 144
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 167
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
b)
Ver solução completaQuestão 168
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
c)
Ver solução completaQuestão 169
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
d)
Ver solução completaQuestão 170
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
a)
Ver solução completaQuestão 171
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
e)
Ver solução completaQuestão 172
1. Dadas as funções abaixo, encontre seu domínio, contra-domínio e imagem.
f)
Ver solução completaQuestão 174
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 175
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 176
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 177
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 178
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 179
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 180
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 181
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 182
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 183
Dadas as funções abaixo, encontre seu domínio, contradomínio e imagem.
Ver solução completa
Questão 184
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 185
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 186
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 187
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 188
Com base no domínio, contradomínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função
Ver solução completa
Questão 189
Sejam os vetores em e e consideremos
a) Qual a distância da origem a esta reta.
Ver solução completaQuestão 191
Para ir de um ponto a um ponto diametralmente oposto de uma piscina circular de de diâmetro, uma pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (vide Figura 3b). Seja o ângulo . Sabendo que ela pode caminhar duas vezes mais rápido do que pode nadar, determine, em termos de , as trajetórias que o levam ao seu destino no maior e no menor tempo. (Observação: considere que a pessoa pode somente caminhar ou somente nadar).
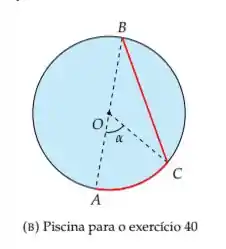
Questão 199
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
a)
Ver solução completaQuestão 200
1.1. Para cada função dada, determine o domínio e faça um esboço dele:
f)
Ver solução completa