Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.14 - Ex. 22a
Verificar quais das seguintes curvas são suaves:
a)
Passo 1
A ideia nessa questão é verificar no esboço da curva se há algum ponto anguloso, isto é, um bico. Vem comigo! A curva que ele nos deu foi a seguinte:
Esboçando o comportamento da curva:
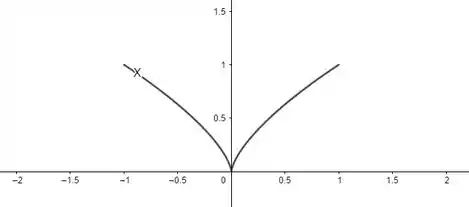
Repare que temos um ponto anguloso em na origem. Assim, nossa curva não será suave
Resposta
Não é suave
Exercícios de Livros Relacionados
Verificar quais das seguintes curvas são suaves:e) r → t = 2 cos t ,3 s e n t , t ∈ 0 ,2 π
Verificar quais das seguintes curvas são suaves:d) r → t = 3 cos 3 t ,3 s e n 3 t , t ∈ π 6 , π 3
Verificar quais das seguintes curvas são suaves:c) r → t = 2 t - s e n t i → + 2 1 - cos t j → , t ∈ π , 3 π
Verificar quais das seguintes curvas são suaves:b) r → t = t 3 i → + t 2 j → , t ∈ 1 2 , 1
Verificar quais das seguintes curvas são suaves:b) r → t = t 3 i → + t 2 j → , t ∈ 1 2 , 1