Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 50

Encontre ∫ 0 5 f x d x se

f x = 3     p a r a   x < 3 x       p a r a   x ≥ 3

Passo 1

Oi, galera! Para calcularmos a integral definida

∫ 0 5 f x d x ,

que tal começarmos olhando o gráfico da função f ( x ) ? Confere aqui embaixo.

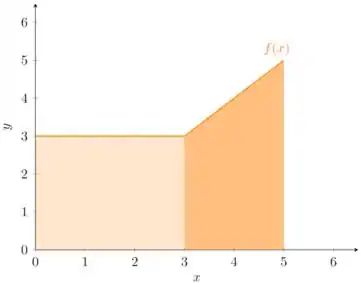
Consegue perceber que a mudança de comportamento da função no ponto x = 3 , dá origem a duas regiões distintas: um retângulo e um trapézio. Então, a integral total pode ser decomposta da seguinte maneira:

∫ 0 5 f x   d x =   ∫ 0 3 f x   d x +   ∫ 3 5 f x   d x ,

pois [ 0,3 ] e [ 3,5 ] são intervalos adjacentes. Além disso, a função f ( x ) é positiva, então podemos resolver o problema por partes, da seguinte forma:

  • Calculando a área de 0 até 3 , onde f x = 3 .
  • Calculando a área de 3 até 5, onde f x = x .
  • Somando os valores das áreas dessas duas regiões.

Passo 2

Vamos começar pela integral mais simples,

∫ 0 3 f x d x .

Essa integral representa a área de um retângulo com base medindo 3 e altura medindo 3 , como podemos ver no gráfico.

Lembra como calculamos a área de um retângulo? Simplesmente multiplicamos o comprimento da base pelo comprimento da altura.

∫ 0 3 f x d x = 3 × 3 = 9 .

Passo 3

Agora vamos para a segunda parte: calcular a integral de 3 a 5 , onde a função é definida como f ( x ) = x .

Olhando para o gráfico, vemos que essa integral representa a área de um trapézio com bases medindo f 3 = 3 e f 5 = 5 , e altura medindo 2 (comprimento do intervalo [ 3 ,   5 ] ).

Lembra como calcular a área de um trapézio? A fórmula é:

Á r e a =   B + b ⋅ h 2 ,

onde B e b são as medidas das bases e h a medida da altura.

Aplicando os valores no nosso problema, chegamos a seguinte igualdade:

∫ 3 5 f x   d x = 5 + 3 ⋅ 2 2 = 8 .

Passo 4

Agora só precisamos juntar os resultados obtidos no Passo 2 e no Passo 3. Vimos que a integral total pode ser decomposta da seguinte forma:

∫ 0 5 f x   d x =   ∫ 0 3 f x d x +   ∫ 3 5 f x d x ,

com

∫ 0 3 f x d x = 9 ,

e

∫ 3 5 f x d x = 8 .

Substituindo os respectivos valores, chegamos ao resultado:

∫ 0 5 f x   d x = 9 + 8 = 17 .

Resposta

∫ 0 5 f x   d x = 17 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →
Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →
Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →
Determine a fórmula para a soma de Riemann obtida dividindo o intervalo [ a , b ] em n subintervalos iguais e usando a extremidade direita para cada c k . Depois, tome o limite dessas somas quando n →
Suponha que int_(- 3)^0 g (t) d t = sqrt(2) . Calcule:int_0^(- 3) g (t) d t int_(- 3)^0 g (u) d u int_(- 3)^0 [- g (x)] d x int_(- 3)^0 (g ( r ))/(sqrt(2)) d r