Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 35
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas.
Passo 1
Bom galera, vamos primeiro plotar o gráfico com as curvas que nos foi dada:
Ele fica com essa “carinha”:
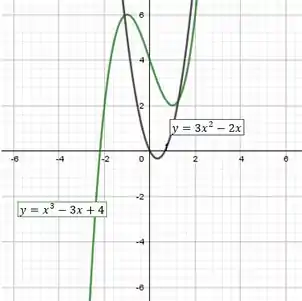
Aqui, para este gráfico, foi utilizado o programinha GeoGebra.
Passo 2
A partir do gráfico, vemos que as curvas se cruzam em:
com em e em .
Passo 3
Portanto, a área da região delimitada pelas curvas é:
Substituindo os valores, temos que a área é:
Resposta
Exercícios de Livros Relacionados
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Use o método de Newton (Seção 4.7), quando necessário, para aproximar as coordenadas x das intersercções das curvas com pelo menos quatro casas decimais; em seguida, use isso para aproximar a área da
Suponha que f e g sejam contínuas em [ a , b ] e que os gráficos de y = f ( x ) e y = g ( x ) se cruzem várias vezes. Descreva um procedimento passo a passo para determinar a área delimitada pelos grá
Suponha que R e S sejam duas regiões no plano x y situadas entre duas retas L 1 e L 2 paralelas ao eixo y . Suponha que cada reta paralela ao eixo y entre L 1 e L 2 intersecte R e S em segmentos de re