Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 27
Encontre uma fórmula explícita para e use-a para fazer na mesma tela os gráficos de , e da reta . Para verificar seu trabalho, veja se seus gráficos de e são reflexões em torno da reta.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar uma fórmula para a função inversa da função e esboçar os gráficos da duas, junto com a reta , na mesma tela.
Pra isso, vamos seguir o passo a passo para encontrar a inversa de uma função:
Então, basicamente vamos isolar e escrever a expressão em função de , beleza?
Vamos lá!
Passo 2
Vamos começar dando uma olhadinha na nossa função:
Escrevendo :
Agora vamos isolar na equação, escrevendo-a em termos de :
Tirando a raiz quarta dos dois lados, vamos ter:
Para , porque , segundo o enunciado.
Agora trocando por , temos a equação resultante da inversa da nossa função:
Passo 3
Com isso, vejamos os gráficos comparados:
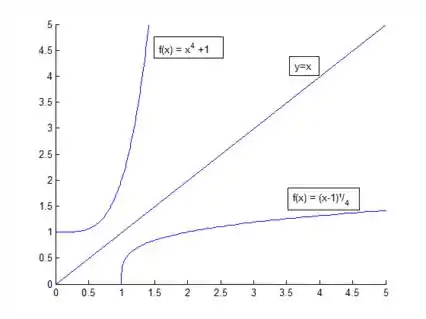
Assim, podemos ver claramente que é a reflexão a curva em torno da reta .
Valeu, galera! Até a próxima! 😉