Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 47
A função sinal, denotada por sgn, é definida por:
- Esboce o gráfico dessa função.
- Encontre ou explique por que não existe cada um dos limites a seguir.
Passo 1
Eaeee, belezinha?? Bom... a questão nos dá a seguinte função:
Queremos esboçar o gráfico dessa função.
Para isso, temos que observar bem os intervalos de que são mencionados nela.
Também queremos resolver os seguintes limites:
Para isso, precisamos saber dos limites laterais!!
Mas o que são esses limites??
Basicamente eles descrevem o comportamento de uma função em relação a um ponto específico, considerando abordagens à direita e à esquerda desse ponto.
Dessa forma, o nosso limite só existe se os limites laterais forem iguais!!
E aí?? Bora lá?? 😉
Passo 2
Bom... perceba que nossa função tem comportamentos:
- Quando a função será constante e igual a ;
- Quando a função será o único ponto ;
- Quando a fun��ão será constante e igual a .
Assim, o gráfico de é dado abaixo:
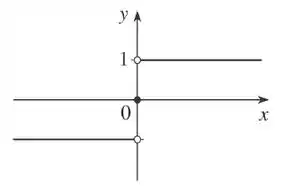
Passo 3
(b)
Pelo gráfico temos:
Pois quando caminhamos para zero pelo eixo positivo é esse valor que encontramos.
Pelo gráfico temos:
Pois quando caminhamos para zero pelo eixo negativo é esse valor que encontramos.
Como os limites laterais são diferentes, temos:
não existe
Passo 4
Aqui também temos que olhar para o limite de ambos os lados.
Sabemos que o módulo “transforma” o número negativo em positivo.
Dessa forma, temos que:
Como os limites são iguais, então:
Entendeu direitinho?? Responde aee 😉
Resposta
-
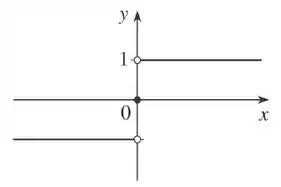
- i)
ii)
iii) Não existe
iv)