Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 59
Trace um diagrama para mostrar que há duas retas tangentes à parábola que passam pelo ponto . Encontre as coordenadas dos pontos onde essas retas tangentes interceptam a parábola.
Passo 1
E aí, pessoal! 😁
Queremos encontrar o ponto de interseção de cada reta tangente com a parábola dada por
sendo que cada uma dessas duas retas tangentes passa pelo ponto .
Parece complicado? 👀
Derivando a função obtemos a expressão para o coeficiente angular das retas tangentes, assim:
em que é o ponto de interseção.
Veja só! 😇
Passo 2
Derivando pela regra da potência para obter , temos
Fazendo primeiramente um esboço, nos ajudará a visualizar a situação:
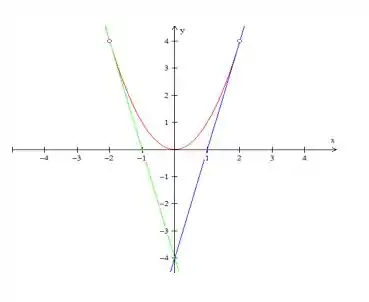
Tranquilo até aqui? 😉
Passo 3
Pelo esboço, percebe-se que a ordenada do ponto de interseção será a mesma para as duas retas tangentes e as abscissas serão simétricas e .
A equação de uma reta tangente que passa por é dada por:
A interseção dessa reta com a parábola é o ponto como vemos pelo gráfico.
Então, fazendo a interseção da parábola com uma das retas tangentes temos a seguinte equação para resolver em :
Como o ponto pertence tanto à tangente como à parábola, então podemos substituir esse ponto na equação, assim:
Logo, temos que
e
E os possíveis pontos de interseção são e
E aí! entendeu tudo? Responde Aí! 😬
Resposta
e