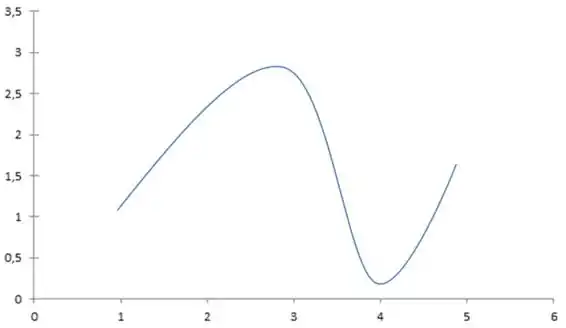
Encontre o gráfico da função f contínua no intervalo [1, 5] com as seguintes propriedades.
Máximo absoluto em 3 e mínimo absoluto em 4;
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??
Vamos analisar o que nosso probleminha está falando. Bom, ele nos pede para montar um gráfico com esses pontos de máximo e mínimo de uma função contínua, ou seja, com pedaços como se fizessem uma parábola.
O que vamos fazer basicamente é montar o gráfico de uma função contínua com 2 concavidades. O máximo absoluto vai estar em , esse vai ser o ponto máximo de uma das concavidades e vai ser o maior valor possível da função.O mínimo absoluto vai estar em , esse vai ser o menor ponto da função e vai estar no ponto mínimo de uma das concavidades.
E aii, partiu??
Passo 2
Nosso primeiro passo vai ser determinar em que ponto vai começar. Como ele nos diz o intervalo, nosso gráfico vai começar no .
Depois dele, vamos ter um máximo absoluto no . Ou seja, a função vai crescendo até chegar em e chega no seu maior valor possível.
E seguimos para um mínimo absoluto no . Sendo assim a função vai diminuir até chegar no mínimo. (que precisa ser o menor ponto em toda a função, pois é o mínimo absoluto.)
Assim, precisamos seguir pro 5, seguiremos crescendo até chegar em que é o fim do nosso intervalo.
Agora podemos montar nosso gráfico!!
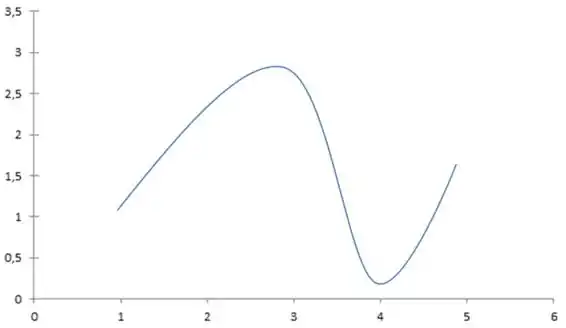
Resposta