Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 16
- Encontre os intervalos nos quais é crescente ou decrescente.
- Encontre os valores máximo e mínimo local de .
- Encontre os intervalos de concavidade e os pontos de inflexão.
Passo 1
Alô, alô, tudo certo com você?
Aqui iremos trabalhar os pontos importantes da função dada que é:
Primeiro, queremos os intervalos onde ela é crescente e decrescente.
Ela vai ser crescente quando a sua derivada for positiva
E decrescente quando sua derivada for negativa
Depois queremos os máximos e mínimos locais.
Para isso encontramos os pontos críticos da função, que é onde a derivada é igual a zero.
E então verificamos, se antes do ponto a derivada é positiva e depois negativa, é um ponto de máximo, pois a função crescia, chegou no máximo e depois decresce.Se for o contrário, o ponto é de mínimo, pois aí a função decrescia, chegou no mínimoe então passou a crescer.
Por fim, para encontrar os intervalos de concavidade, vamos derivar de novo, para encontrar a segunda derivada.
Se a segunda derivada for positiva, a função é côncava para cima:
Se a segunda derivada for negativa, a função é côncava para baixo:
E quando a segunda derivada é nula, isso indica um ponto de inflexão:
Bora lá?
Passo 2
Para achar os intervalos vamos calcular a primeira derivada, e analisar os sinais:
Vamos usar as regras de derivação do produto, do polinômio e da função logarítmica:
Vamos agora aplicar:
Vamos igualar a zero, para encontrar os pontos críticos e o ponto onde a derivada passa de ser positiva para negativa e vice-versa.
Dessa forma, temos que:
Ou
E elevando pela exponencial dos dois lados, temos:
Portanto, outro ponto crítico é:
No entanto, a função não é definida em , uma vez que a função é dada por:
E não existe logaritmo natural de número negativo ou de zero, o domínio de é apenas para .
Com isso, o único ponto crítico é o ponto
Avaliando os intervalos de crescimento temos:
Passo 3
Para ser um ponto de máximo ou mínimo local, o sinal de deve mudar nesse ponto.
Vemos que em há mudança do sinal de , e como em o sinal muda de negativo para positivo, então ele é um ponto de mínimo local.
Para achar os valores é só substituir os valores em :
Passo 4
Para achar os intervalos de concavidade devemos achar e analisar os sinal vamos derivar:
Essa é a nossa segunda derivada.
E fazendo o mesmo processo, vamos igualar a zero:
Avaliando o comportamento da segunda derivada antes e depois de
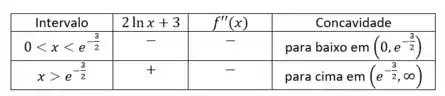
Para garantir que é ponto de inflexão, devemos ver se existe:
Temos que o ponto de inflexão é .
Resposta
- Decrescente em e crescente em
- é mínimo local
- Concavidade para baixo em e para cima em e ponto de inflexão é