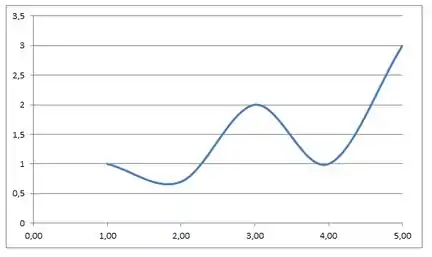
Encontre o gráfico da função contínua no intervalo [1, 5] com as seguintes propriedades.
Máximo absoluto em 5, mínimo absoluto em 2, máximo local em 3 e mínimos locais em 2 e 4
Passo 1
Opa, e aí! Tudo bem?! Aqui temos que construir um gráfico que obedeça a algumas características:
- Mínimo absoluto em ;
- Máximo local em ;
- Mínimos locais em e ;
- Máximo absoluto em .
Essa função tem que está no intervalo
Então a gente vai juntar essas informações e, sabendo onde a função assume valores maiores ou menores, a gente pode descobrir quando ela é crescente e quando é decrescente.
Passo 2
Queremos então uma função que começa decrescente até , esse deve ser o menor valor da função. Nesse ponto ela começa a crescer até e volta a decrescer até . Por fim a função cresce novamente até o valor máximo em .
Não precisamos da função, apenas do gráfico! Então é só soltar a imaginação e desenhar!
Agora podemos montar nosso gráfico:
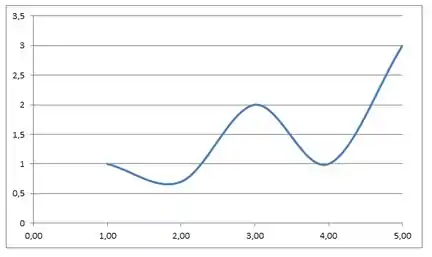
Prontinhoo!
Resposta