Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 3
- Encontre a inclinação da reta tangente à parábola no ponto
- Usando a definição 1
- Usando a equação 2
- Encontre a equação da reta tangente da parte (a)
- Faça os gráficos da parábola e da reta tangente. Como verificação, dê um zoom em direção ao ponto até que a parábola e a reta fiquem indistinguíveis.
- Usando a definição 1
- Usando a equação 2
Passo 1
Opa, bora resolver esse problema!
O enunciado nos pede pra encontrarmos a inclinação da reta tangente à parábola no ponto de diferentes formas:
Primeiramente, resolveremos usando a definição 1, que utilizar essa forma de limite:
E depois usamos a definição 2, que usa essa outra forma de limite:
Em ambas as definições, é o ponto da reta tangente na curva dada e é a curva dada.
Já para encontrarmos a equação da reta tangente, iremos utilizar a formula:
Em que é o ponto que nos é fornecido.
Veja só! 😁
Passo 2
Letra a)
Substituimos a função na definição 1, temos:
Como queremos no ponto , então :
Substituindo :
Se a gente substituir agora caímos em uma indeterminação de divisão por zero, então temos que dar um jeito de fugir dessa indeterminação.
Podemos fatorar o numerador para vermos se conseguimos uma simplificação:
Logo podemos rescrever nosso polinômio como:
Assim podemos simplificar e retirar a indeterminação:
Tranquilo até aqui? 🤔
Passo 3
Agora, resolveremos usando a equação 2:
Temos que:
E:
Substituindo e calculando:
Realizando o produto notável:
Simplificando os termos semelhantes:
Simplificando :
Aplicando o limite:
Prontinho, chegamos na mesma resposta!
Bacana, não é? 😉
Passo 4
Letra b)
Pra encerrar temos que fazer um gráfico de e de sua reta tangente. Mas quem é a reta tangente?!!
Conhecemos sua inclinação:
Para encontrar a sua expressão fazemos:
Conhecemos o ponto :
Estamos quase lá! 😬
Passo 5
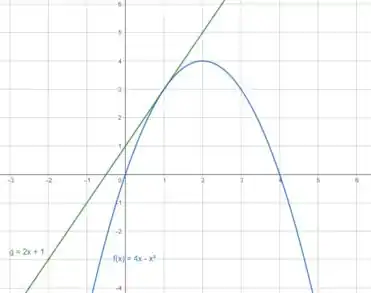
Esboçando os gráficos com o auxilio do GeoGebra:
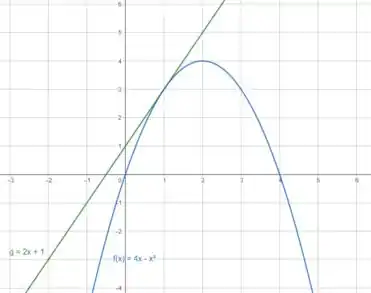
Agora, dando um zoom no ponto :
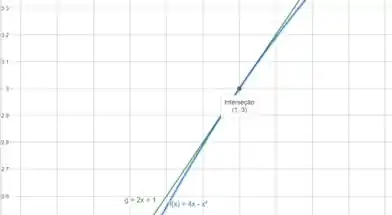
Repara que nossa parábola se aproxima de uma reta quando damos zoom.
Entendeu tudo? Responde Aí! 😇
Resposta
