Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 42
- Encontre os intervalos em que a função é crescente ou decrescente.
- Encontre os valores máximo e mínimo locais.
- Encontre os intervalos de concavidade e pontos de inflexão.
- Use as informações de a)-c) para esboçar o gráfico.
Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da função. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, já que a derivada é negativa.
No item (b), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (c) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (d) vamos usar as informações das partes (a)-(c) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Vamos resolver por ordem dos itens, beleza?
No item a) precisamos achar onde cresce ou decresce, mas pra isso precisamos da derivada e dos pontos críticos, então vamos encontra-los.
Sendo nossa função:
Derivando , usando a regra do expoente em cada termo, temos que
Precisamos achar nossos candidatos a máximo e mínimo, ou seja, pontos críticos.
Ou seja,
Isto é,
ou
Ou seja,
Então e são candidatos a pontos críticos.
Passo 3
Agora, precisamos analisar as proximidades desse ponto para usar o teste da primeira e obter os máximos e mínimos (ou não hahah)
Temos que
- se
- se
- se
- se
(você pode verificar isso pegando números no intervalo que te dei e aplicando na derivada).
Pelo teste da primeira derivada, é crescente em e e decrescente em e .
Passo 4
Respondendo o item b)...
Vamos usar o item anterior, olha só!
é um máximo local, pois sai de crescente para decrescente. E, é um mínimo local, pois sai de decrescente para crescente.
Passo 5
Precisamos saber da concavidade da função, beleza? Então vamos calcular a segunda derivada.
Usando a regra da subtração, temos que
Achando o candidato a ponto de inflexão
Ou seja,
Colocando em evidencia,
Daí,
ou
Temos que esses são nossos candidatos a ponto críticos
Passo 6
Agora temos que analisar o que acontece nas proximidades do ponto que encontramos no passo anterior, para verificar se ele é mesmo um ponto de inflexão. Vamos lá!
Temos que:
- se
- se
- se
- se
Temos que é conca para cima em e e para baixo em e .
Pelo teste da segunda derivada, não temos um ponto de inflexão
Passo 7
Agora, temos que esboçar o gráfico.
Partiu!
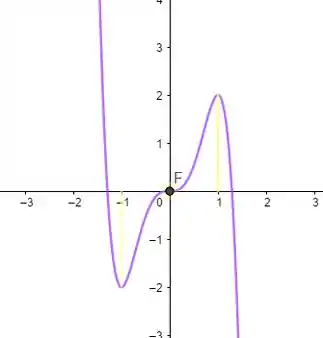
Resposta
é crescente em e e decrescente em e .
é um máximo local. E, é um mínimo local.
Temos que é concava para cima em e e para baixo em e .
Não temos um ponto de inflexão
Conferindo com o software, é decrescente em .
