Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 2b

Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de

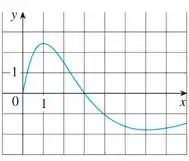
b)

Passo 1

Olá, meu amigo. Pronto para essa resolução?

Aqui a gente tem o gráfico de uma função,

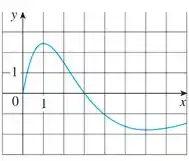
e a partir dele deveremos criar o gráfico da derivada desta função no ponto que é pedido.

Vish! Parece difícil, né? Mas, olha só, vou te contar um negócio! A gente vai fazer e você vai mudar de opinião.

Sabemos que o conceito de derivada, é além do limite, né?!

A derivada representa o coeficiente angular da reta tangente ao ponto que queremos calcular a derivada da função em relação ao eixo .

Resumindo... Vamos ter que desenhar a reta tangente ao ponto e depois tenta estimar o ângulo da reta em relação ao eixo

Passo 2

Mas vamos desenhar primeiro a reta tangente no ponto . A reta deve ser tangente ao gráfico neste ponto.

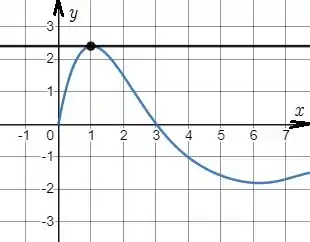
Olha só, a reta tangente é horizontal e quando isso acontece significa que a tangente é paralela ao eixo e quando isso acontece, o coeficiente angular da reta, ou seja, ou ângulo formado entre a reta e o eito , no ponto é zero.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41) Dada f x = x - 3 Use uma calculadora para tabular valores de f 7 + ∆ x - f ( 7 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 7 + ∆ x - f ( 7 )

42) Dada f x = 10 x 2 Use uma calculadora para tabular valores de f 5 + ∆ x - f ( 5 ) ∆ x quando ∆ xé1 ,0,5 ,0,1 ,0,01 ,0,001 , e∆ xé - 1 ,- 0,5 ,- 0,1 ,- 0,01 ,- 0,001 é é . A que f 5 + ∆ x - f ( 5 )

A área da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se f for essa função , ache f(b). Ache também lim b → ∞ ⁡ f ( b )

O volume de um solido de revolução da região limitada pela curva y = e - x , pelos eixos coordenados e pela reta x =b (b0) é uma função de b. Se g for essa função , ache g(b). Ache também lim b → ∞ ⁡

Uma partícula move-se sobre uma reta , sendo s a distancia orientada da partícula a partir da origem , V m/s, a velocidade da partícula e A m/s² , a aceleração da partícula, t s. Se a = e t + e - t ,