Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 34
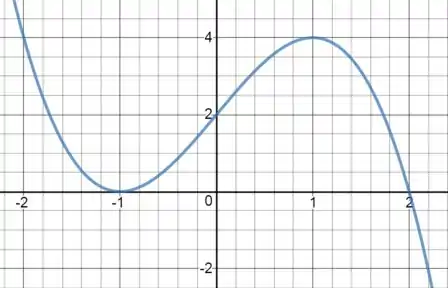
(a) Encontre os intervalos em que a função é crescente ou decrescente.
(b) Encontre os valores máximos ou mínimos locais.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use as informações das partes (a)-(c) para esboçar o gráfico. Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.
Passo 1
Oieee, vamos lá?
Vamos resolver cada parte uma por uma.
(a) Intervalos de Crescimento e Decrescimento
Para encontrar os intervalos onde a função é crescente ou decrescente, precisamos encontrar os intervalos onde a primeira derivada é positiva (crescente) ou negativa (decrescente).
Encontre a primeira derivada:
Encontre os intervalos onde (crescente) e (decrescente):
Para encontrar onde resolvemos a desigualdade:
Isso nos leva a , o que implica .
Portanto, a função é crescente em
Passo 2
(b) Valores Máximos e Mínimos Locais
Para encontrar os valores máximos e mínimos locais, precisamos identificar os pontos críticos, onde a primeira derivada é zero ou indefinida.
Encontre os pontos críticos:
Isso ocorre quando , ou seja, .
Estes são os pontos críticos.
Teste da Derivada Segunda:
A segunda derivada é
Para então é um mínimo local.
Para então é um máximo local.
Passo 3
(c) Intervalos de Concavidade e Pontos de Inflexão
Para encontrar os intervalos de concavidade e os pontos de inflexão, precisamos determinar onde a concavidade da função muda.
Encontre os pontos de inflexão:
Os pontos de inflexão ocorrem quando a segunda derivada muda de sinal.
A concavidade muda em então este é um ponto de inflexão.
Intervalos de Concavidade:
Para determinar os intervalos de concavidade, devemos verificar onde (concave para cima) e (concave para baixo).
Como, a concavidade muda de côncava para cima para côncava para baixo em
Passo 4
(d) Esboço do Gráfico
Com todas essas informações:
- A função é crescente em
- Há um máximo local em e um mínimo local em
- Há um ponto de inflexão em
- A função é côncava para cima em e côncava para baixo em
Com essas informações, podemos esboçar o gráfico da função.
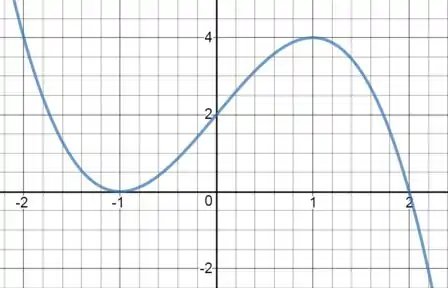
Resposta
(a) é decrescente para valores de nos intervalos e e crescente no intervalo .
(b) é ponto de mínimo local e é ponto de máximo local.
(c) possui concavidade para baixo para valores de no intervalo e concavidade para cima para valores de no intervalo . E o ponto de inflexão é .
(d)
