Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 41
Encontre o limite ou demonstre que ele não existe:
Passo 1
Fala aí, pessoal! 😊
Nesse problema queremos obter o limite
Tem ideia do que fazer? 😬
Se aplicarmos o método de substituição diretamente vamos cair em uma indeterminação .
Então para solucionar essa questão podemos aplicar uma propriedade logarítmica para facilitar nossa vida...
Veja só! 😎
Passo 2
Beleza, se a gente usar essa propriedade dos logaritmos, a gente vai facilitar nosso cálculos:
Agora, a gente pode colocar em evidência os da fração:
Continuando, podemos aplicar o limite nas frações dentro do parênteses pra eliminar porque a gente sabe que:
Então a gente aplica isso no limite:
Tranquilo até aqui? 😊
Passo 3
Por fim a gente aplica o limite, pra ajudar a gente a desobrir o limite de , a gente pode olhar o gráfico:
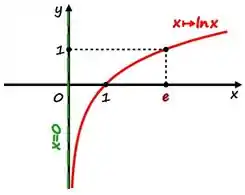
Como a função cresce indefinidamente, então:
E aí! entendeu tudo? Responde Aí! 😇
