Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 44d
Para encontre cada o seguinte limite:
Passo 1
Fala aí, pessoal. Tudo certinho com você?
Bom, a questão deu pra gente a função
E pediu pra gente calcular o limite
Perceba que esse é um limite lateral, onde o está se aproximando de pela direita.
Vamos aplicar as propriedades de limite e ver o que vai rolar.
Vem comigo.
Passo 2
Bom galera, primeiro vamos separar o limite em dois, porque a gente pode e vai facilitar muito, então vamos por a mão na massa:
Passo 3
Beleza, agora vamos calcular o primeiro limite, ele não tem segredo é só substituir o por e calcular, fica:
Show
Passo 4
Por último a gente calcula o outro limite, mas pra isso a gente tem que pensar um pouquinho sobre logaritmo natural, então vamos olhar o gráfico da função do logaritmo natural:
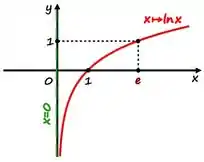
Então quando do tender a pela direita, a função vai tender a por valores positivos, então o inverso disso (que é o que aparece no limite) tende a infinito por valores positivos, ficamos com: