Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 33

Encontre uma parametrização para o círculo x - 2 2 + y 2 = 1 iniciando em (1, 0) e se movendo em sentido horário uma vez ao redor do círculo, com o ângulo central θ na figura a seguir como parâmetro.

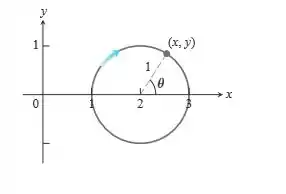
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

O sen ⁡ θ pode ser dado da seguinte forma

sen ⁡ θ = C a t e t o   o p o s t o H i p o t e n u s a = y 1

Portanto,

y = sen ⁡ θ

E para o cosseno, temos que

cos ⁡ θ = C a t e t o   a d j a c e n t e H i p o t e n u s a = x - 2 1

Portanto, nós temos que

x - 2 = cos ⁡ θ

Simplificando as coisas

x = 2 + cos ⁡ θ

Resposta

x = 2 + cos ⁡ θ ,     y = sin ⁡ θ ,     0 ≤ θ ≤ 2 π

Exercícios de Livros Relacionados

Desenhe os gráficos dos conjuntos de pontos cujas coordenadas polares satisfaçam as equações e desigualdades nos Exercícios 11-26. 1 ≤ r ≤ 2
Encontre as coordenadas cartesianas dos seguintes pontos (dados em coordenadas polares). 2 ,π / 4 1 ,0 0 ,π / 2 - 2 ,π / 4 - 3 ,5 π / 6 5 , tg - 1 ⁡ 4 / 3 - 1 ,7 π 2 3 ,2 π / 3
Desenhe os gráficos dos conjuntos de pontos cujas coordenadas polares satisfaçam as equações e desigualdades nos Exercícios 11-26. 0 ≤ θ ≤ π 6 ,r ≥ 0
Encontre as coordenadas polares, - π ≤ θ2 π e r ≤ 0 , dos pontos a seguir dados em coordenadas cartesianas. 3 2 , 1 2
Encontre as coordenadas cartesianas dos pontos do Exercício 1.