Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 42
Encontre os pontos nos quais é descontínua. Em quais desses pontos é contínua à direita, à esquerda ou nenhum deles? Esboce o gráfico de .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
O enunciado pede para identificar os pontos de descontinuidade e em seguida classifica-los quanto a continuidade lateral. Antes de mais nada, devemos observar que é definida por partes e que suas partes são funções contínuas. Assim, os possíveis pontos de descontinuidade são os pontos de “colagem”, que são os pontos em que temos a transição entre as funções diferentes que compõem nossa função.
Vale lembrar também que uma função é contínua lateralmente em um ponto se o limite lateral coincidir com o valor da função no ponto em questão.
Passo 2
Os pontos de “colagem” são e . Primeiramente vamos analisar o que acontece em . À esquerda desse ponto (), , assim o limite lateral à esquerda é
À direita (), , de modo que
Como os limites laterais são diferentes, não existe e é descontínua nesse ponto. Por outro lado, como , é contínua à esquerda nesse ponto.
Passo 3
Analisemos agora o que acontece em . O limite à esquerda será
O limite à direita será
Como os limites laterais são diferentes, o limite não existe e é descontínua nesse ponto. Por outro lado, como , é contínua à direita nesse ponto.
Passo 4
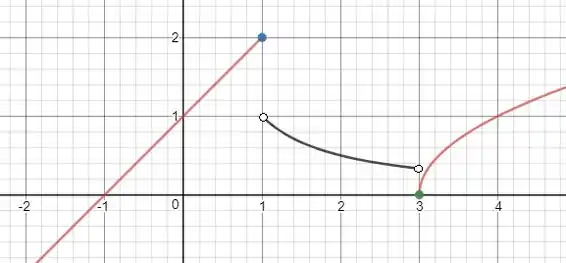
O esboço do gráfico de foi feito com ajuda do nosso amigo GeoGebra:
Resposta
R: é descontínua em (é contínua à esquerda nesse ponto) e e, (é contínua à direita nesse ponto).