Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.10 - Ex. 12
É dada uma função .
a) Determine os valores de tais que .
b) Ache todos os intervalos abertos que contêm um determinado valor de que satisfaça a parte a) tais que para todo em .
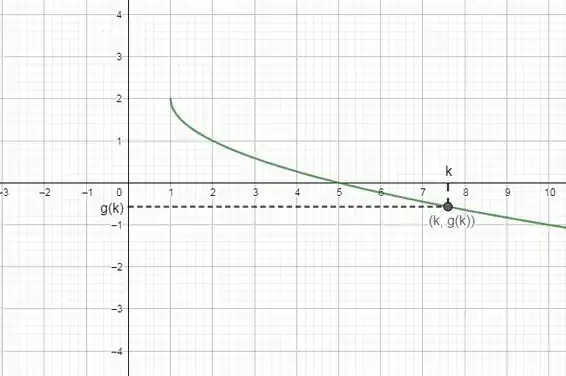
c) Faça um esboço do gráfico de e mostre no gráfico a interpretação geométrica dos resultados das partes a) e b).
Passo 1
Bem, em questões de limites temos que primeiro ver o que ele está pedindo. As vezes pode ser apenas fazer um calculo mais simples. E outras vezes vamos precisar usar truques de cálculo. Desta vez o que ele pede é ver o que acontece se jogarmos nosso valor C no limite. Então vamos la!
Passo 2
Beleza, agora ele quer saber os intervalos de K que cálculos no item a .
Assim sempre que estiver nos intervalos
Passo 3
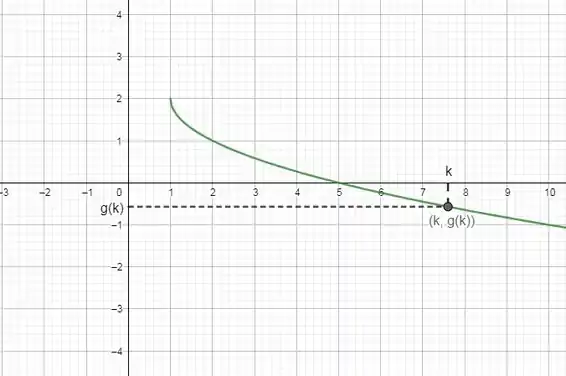
Nossa função tem esse formato. Vemos que todos os valores de nos retornam com uma e qualquer intervalo dentro de satisfaz essa condição
Resposta
a) sempre que estiver nos intervalos
b) Como
c)
