Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.9 - Ex. 4

Encontre a primitiva mais geral da função. ( Verifique sua resposta derivando.)

f = 8 x 9 - 3 x 6 + 12 x 3

Passo 1

E aí! como vai? 😁

Bom, galera... nessa questão estamos interessados em encontrar a primitiva da função f :

f = 8 x 9 - 3 x 6 + 12 x 3

Para isso, iremos utilizar a seguinte tabela de primitivas presente na seção 4.9 .

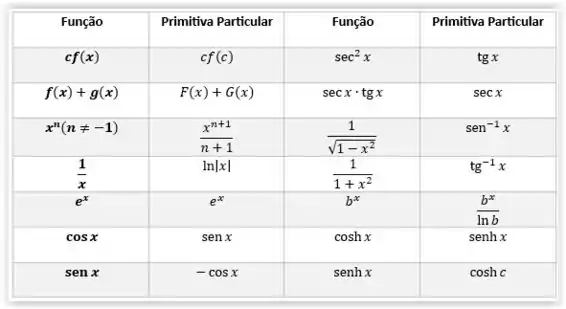
Para encontrar a primitiva de f , iremos utilizar a Regra da Potência, que é

x n = x n + 1 n + 1   p a r a   n ≠ - 1

Veja só! 😊

Passo 2

Aplicando a Regra da Potência em f , temos:

f x = 8 x 9 - 3 x 6 + 12 x 3

F x = 8 1 10 x 10 - 3 1 7 x 7 + 12 1 4 x 4 + C

Ao derivar F ( x ) , temos

F ' x = 8 x 9 - 3 x 6 + 12 x 3

Então como

F ' x = f ( x )

Então F ( x ) é a primitiva de f ( x ) .

E então! O que achou? Responde Aí! 😉

Resposta

F x = 4 5 x 10 - 3 7 x 7 + 3 x 4 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva os problemas de valor inicial nos Exercícios 91-112.
Resolva os problemas de valor inicial nos Exercícios 91-112.
Resolva os problemas de valor inicial nos Exercícios 91-112.
Resolva os problemas de valor inicial nos Exercícios 91-112.
Resolva os problemas de valor inicial nos Exercícios 91-112.