Encontre a primitiva mais geral da função. (Verifique sua resposta derivando.)
Passo 1
Fala galera, nessa questão estamos interessados em encontrar a primitiva da função , e conferir se realmente chegamos na primitiva certa, derivando.
Para isso, iremos utilizar a seguinte tabela:
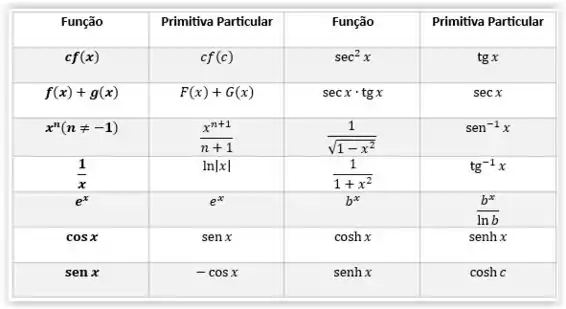
Passo 2
Para encontrar a primitiva de , iremos utilizar a regra da potência, que diz:
Primeiramente vamos deixar a função com uma cara melhor
Vamos dividir todos os seus termos por , mas não podemos esquecer que não podemos dividir por , então temos que o domínio da nossa função é qualquer numero real, exceto o , podemos escrever assim:
domínio
Aplicando regra da potência da primitiva:
Agora vamos deixa-la mais organizada:
Passo 3
Vamos verificar se chegamos a primitiva correta? Então bora derivar essa equação, e para isso usaremos a regra da potência para a derivada, lembra dela?
Ao derivar , temos
Vamos voltar o para o denominador:
Temos enfim:
Logo é a primitiva de !