Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 30
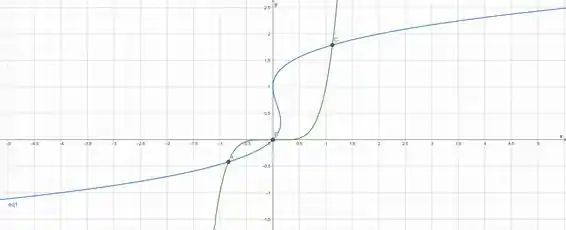
Trace as curvas
E
E encontre seus pontos de interseção, com precisão de uma casa decimal.
Passo 1
Fala, meu bom amigo. Vamos de mais uma resolução hoje?
A questão quer que a gente trace essas curvas com o auxílio de uma ferramenta gráfica.
Para isso, vamos parametrizar essas funções como funções explícitas (faço isso porque entendo que é assim que o livro quer que a gente faça, mas você não precisa necessariamente fazer dessa forma pra chegar na resposta final da questão, beleza?)
Para gerarmos os gráficos de cada uma, irei utilizar o GeoGebra, mas você pode utilizar qualquer software matemático que o resultado será o mesmo.
Para encontrarmos a intersecção entre ambas as figuras, o que iremos fazer é substituir a equação de uma na outra, isso nos trará o ponto de intersecção entre elas.
Passo 2
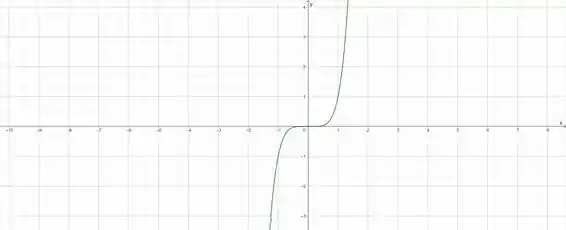
Para a primeira curva temos:
E seu esboço fica:
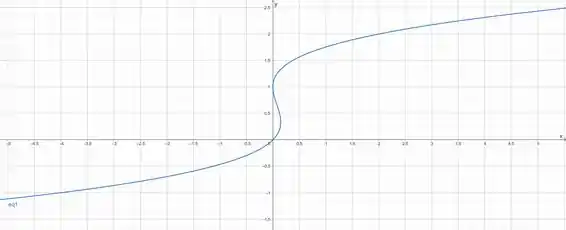
Já para a segunda curva, temos:
E seu esboço fica:
Passo 3
Agora para acharmos os pontos de interseção entre elas, podemos simplesmente substituir a primeira na segunda:
E chegamos numa parada que vai ser meii cabeluda de resolver na mão.
Mas, felizmente a questão é uma questão de resolução gráfica.
E aí, lá no nosso software, (eu to usando o Geogebra), a gente pode pedir a interseção, e ele vai nos dar os seguintes pontos, com precisão de uma casa decimal:
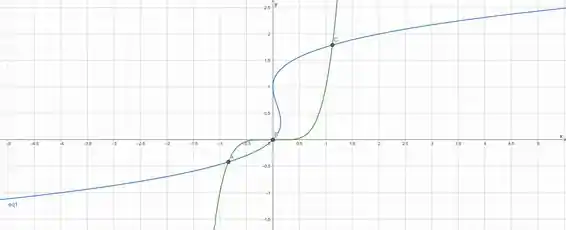
Resposta
