Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.5 - Ex. 12
- Encontre o valor médio de no dado intervalo.
- Encontre cujo
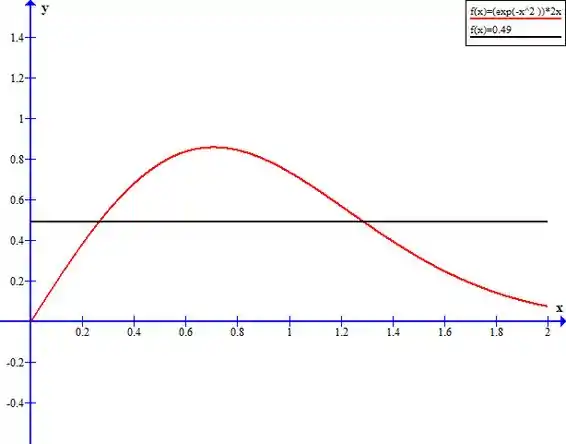
- Esboce o gráfico de e o retângulo cuja área é a mesma da área abaixo do gráfico de
Passo 1
(a) Pessoal, nesta seção nos é dado o conceito de valor médio da função em um intervalo [a,b]. Ele é o seguinte:
Então, para resolver o exercício devemos substituir o valor da função e seu intervalo na equação dada:
Primeiramente, vamos fazer uma substituição de variável (de modo muito estratégico rsrs). Seja:
Aplicando na integral (Vamos esquecer o intervalo por agora):
Substituindo o valor de e aplicando o intervalo [0,2]:
Passo 2
(b) Agora temos que achar um valor tal que . Vamos aplicar esta igualdade:
Para encontrar as raízes desta equação, será necessário o uso de um software computacional. A partir deles temos que:
Passo 3
(c) A área abaixo do gráfico vale:
A área do retângulo deve ser a mesma, então:
Resposta
Exercícios de Livros Relacionados
Use o teorema do valor médio para integrais para provar a desigualdade: ∫ - π / 6 π / 6 cos 2 x d x ≤ π 3
Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ 2 4 x 2 = 56 3
Use o teorema do valor médio para integrais para provar a desigualdade: 0 ≤ ∫ - 1 / 2 1 / 2 cos π x ≤ 1
Use o teorema do valor médio para integrais para provar a desigualdade: ∫ 0 2 1 x 2 + 4 d x ≤ 1 2
Use o teorema do valor médio para integrais para provar a desigualdade: ∫ 0 π sen x d x ≤ π