Encontre os valores máximos e mínimos absolutos de no conjunto .
,
é um quadrilátero com vértices:
, , e
Passo 1
Oie, vamos de resolução hoje.
Aqui a gente tem a função:
Neste exercício, precisamos encontrar e classificar os pontos críticos da função dentro de um conjunto :
é um quadrilátero com vértices:
, , e
Abaixo a gente pode ver a região que estamos trabalhando:
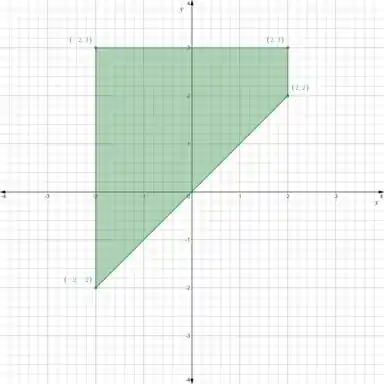
Para determinar os valores máximo e mínimo absolutos de uma função contínua em um conjunto fechado e limitado :
1. Determine os valores de nos pontos críticos de em .
2. Determine os valores extremos de na fronteira de .
3. O maior dos valores dos passos e é o valor máximo absoluto; o menor desses valores é o valor mínimo absoluto
Passo 2
Bom galera, vamos começar calculando os pontos críticos que são encontrando em:
Pegando as derivadas parciais são:
Encontrando suas raízes:
E agora iremos encontrar :
E suas raízes:
Com isso, temos os pontos críticos:
, , e
Vamos olhar quais pontos estão dentro da região :
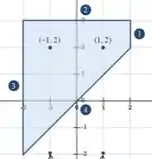
São os pontos:
e
Passo 3
Beleza, vamos calcular a função nesses pontos:
E para o segundo ponto:
Passo 4
Agora vamos testar também as fronteiras do nosso intervalo. A primeira fronteira é dada pela equação e intervalo:
Nesse ponto da fronteira temos que:
E
E no ponto crítico nessa fronteira:
Calculando a derivada:
Calculando o zero:
Então desde que então:
E
Passo 5
Agora pra o intervalo , na fronteira :
Nesse ponto da fronteira:
E no outro extremo:
Agora iremos calcular o ponto crítico:
Calculando a derivada:
Calculando o ponto crítico:
E agora vamos encontrar o valor da função no ponto crítico que encontramos:
E
Passo 6
Agora na fronteira , no intervalo , teremos:
Nos pontos extremos da fronteira:
E
E iremos encontrar os pontos críticos:
Calculando o ponto crítico:
Temos então que a raiz é:
E agora a gente encontra o valor da função nesses pontos críticos:
E
Vamos para o último valor da fronteira, no intervalo :
Vamos encontrar apenas os pontos críticos pois na fronteira desse intervalo a gente já calculou:
Calculando a derivada:
E então aqui não temos candidatos para máximos ou mínimos.
Então, por todos os valores que encontramos, temos que:
Minimo:
Máximo:
Resposta
Minimo:
Máximo: