Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.4 - Ex. 23
Utilize a tabela do Exemplo 3 para encontrar a aproximação linear da função humidex quando a temperatura está próxima de e a umidade relativa do ar é de aproximadamente . Estime também o humidex quando a temperatura é de e a umidade relativa, .
Passo 1
Então galera, a tabela do exemplo 3 é essa aqui ó:
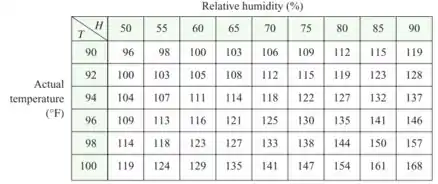
De acordo com a tabela acima, temos que . Aqui vale ressaltar que é uma função da seguinte forma: , ok? No entanto, o que queremos é a aproximação linear da fução humidex, então teremos que determinar a derivada nesse ponto, que pode ser calculada da seguinte forma:
Aproximando para e utilizando os valores da tabela, teremos:
Sendo assim, podemos concluir que .
Passo 2
Similarmente ao que fizemos com a função temperatura, para a função humidex temos que a derivada será:
Aproximando para e utilizando os valores da tabela, teremos:
Sendo assim, podemos concluir que .
Passo 3
Agora que encontramos as derivadas no ponto, fazendo a aproximação linear:
Para e , teremos:
E essa é a nossa resposta final! 😉