Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.5 - Ex. 62
Encontre . Verifique se sua resposta é razoável comparando os gráficos de e .
Passo 1
Pessoal, nessa questão, queremos encontrar a derivada da função
E então comparar o gráfico da derivada com o da função e ver se faz sentido.
Para deriva-la, vamos lembrar que a função arcotangente, possui derivada dada por:
Nesse caso, temos uma função dentro do argumento da arcotangente, portanto, faremos a regra da cadeia:
Passo 2
Temos que a derivada de é dada por:
Agora fazendo o gráfico de ambas as funções temos o seguinte:
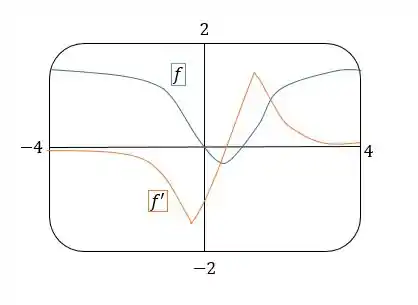
O que faz sentido, pois a derivada é negativa quando a função decresce e positiva quando ela cresce. Além disso, a derivada vale zero no ponto onde a função possui um mínimo e portanto reta tangente horizontal.
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 13 a 20, ache uma equação da reta tangente a curva dada, no ponto indicado. Faça um esboço da curva com a reta tangente e a reta norma.18)y = 2 x - x 3 ; ( - 2,4 )
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde
Nos exercícios de 1 a 6, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m no intervalo fechado [ a , b ] e inclua na tabela os pontos onde
Nos exercícios de 7 a 12, ache a inclinação da reta tangente ao gráfico no ponto ( x 1 , y 1 ) . Faça uma tabela de valores de x, y e m nos vários pontos do gráfico e inclua na tabela os pontos onde o