Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 26
a) Faça o gráfico da função
b) Explique a forma do gráfico calculando o limite quando ou quando .
c) Estime os valores máximo e mínimo e então use o cálculo para achar os valores exatos.
d) Use o gráfico de para estimar a coordenada dos pontos de inflexão.
Passo 1
Fala aí, tudo certinho com você?
Bom, nessa questão nos é dada a função
E precisaremos responder a alguns itens sobre ela.
No item a) precisaremos fazer o gráfico dessa função. Como essa é uma função mais complicadinha, usaremos um programinha de computador para isso.
No item b) precisaremos explique a forma do gráfico calculando o limite quando ou quando .
No item c) teremos que estimar os valores máximo e mínimo e então use o cálculo para achar os valores exatos. Ou seja, vamos olhar os valores no gráfico encontrado no item a) e depois usar a derivada da função igualada a zero para descobrir seus pontos de máximo e de mínimo.
Já no item d) precisaremos usar o gráfico de para estimar a coordenada dos pontos de inflexão. Para isso devemos lembrar que o ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero. Assim:
Perfeito. Agora que já sabemos o caminho, vamos resolver cada um dos itens pedidos.
Passo 2
Item a). a função que estamos analisando é:
Perceba que essa função é contínua quando , que é no intervalo de formato , então nós esboçamos um gráfico de com limites . E ele terá essa carinha aqui:
Maravilha.
Passo 3
Item b). Agora vamos explicar a forma do gráfico calculando o limite quando ou quando .
Conseguimos usar a seguinte propriedade do logaritmo, aplicando dos dois lados da equação:
Assim:
Assim podemos facilitar nosso cálculo de limite.
Fazendo:
E podemos escrever . Assim, nosso limite se torna:
Mar isso cairá em uma indeterminação. Então vamos aplicar a regra do L’Hospital, derivando a função de cima e a função de baixo e tentando recalcular o limite.
Assim, teremos:
E simplificando, ficamos com:
Assim, concluímos que:
Show.
Passo 4
Item c). Aqui teremos que estimar os valores máximo e mínimo e usar o cálculo para achar os valores exatos.
Ou seja, vamos olhar os valores no gráfico encontrado no item a) e depois usar a derivada da função igualada a zero para descobrir seus pontos de máximo e de mínimo.
Pelo gráfico, parece haver um máximo local em , e mínimos locais em , e em .
Como:
Podemos usar novamente
E calculando sua derivada implicitamente, temos:
Que pode ser escrita com:
Assim, isolando , termos:
E substituindo
Agora vamos ver o que acontece quando
temos que ou ou .
No intervalo e .
Aproximando esses pontos nos dá que
e
Essas aproximações confirmam nossa estimativa.
Passo 5
Por fim, no item d) precisamos usar o gráfico de para estimar a coordenada dos pontos de inflexão.
Para isso devemos lembrar que o ponto de inflexão acontece onde a derivada de segunda ordem for igual a zero.
O gráfico de é o seguinte:
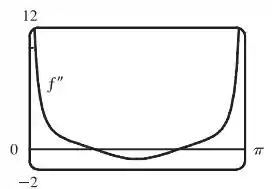
Pelo gráfico, nós vemos que em e .
Como troca o sinal nesses valores, eles são coordenadas dos pontos de inflexão.
E assim, encerramos mais uma questão.
Resposta
No desenvolvimento.