Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 29
- A partir do gráfico da função e dando zoom no ponto em que o gráfico cruza o eixo , estime o valor de
- Verifique sua resposta da parte (a), calculando para valores de que se aproximem de .
Passo 1
Eaeee, belezinha?? Bom... a questão quer que estimemos o valor do seguinte limite dando zoom no ponto em que o gráfico cruza o eixo :
Dado que:
Depois a função quer que verifiquemos a resposta calculando para valores de que se aproximem de .
E aí?? Bora lá?? 😉
Passo 2
- Esboçando o gráfico de , temos o resultado abaixo:
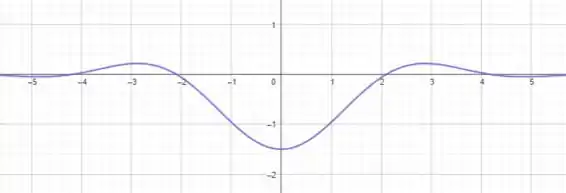
Dando um zoom nele, obtemos:
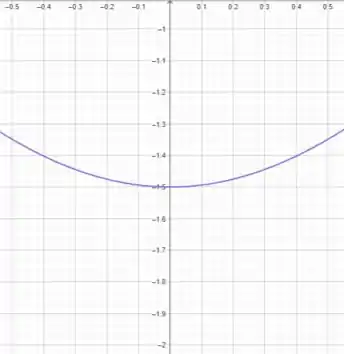
Logo, verfica-se que
Passo 3
Para verificar o resultado obtido em (a), pegamos valores próximos de zero para e aplicamos na função . Obtemos assim o seguinte resultado tabelado abaixo:
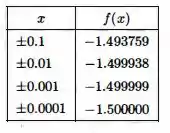
Isso nos mostra que é válida a resposta obtida (a) .
Resposta
Exercícios de Livros Relacionados
Determine os limites nos Exercícios 23-42. lim x → 5 x - 5 x 2 - 25
Determine os limites nos Exercícios 23-42. lim x → 1 x - 1 x + 3 - 2
Determine os limites nos Exercícios 11-22. lim x → - 7 ( 2 x + 5 )
Determine os limites nos Exercícios 23-42. lim x → - 2 - 2 x - 4 x 3 + 2 x 2
Determine os limites nos Exercícios 23-42. lim t → - 1 t 2 + 3 t + 2 t 2 - t - 2