Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 23
Encontre os vértices, os focos e as assíntotas da hipérbole e esboce seu gráfico.
Passo 1
Oieee, tudo bem? Vamos de resolução de mais uma atividade. Hoje iremos resolver uma atividade sobre hipérbole.
Dada a equação geral:
Precisamos encontrar os vértices, os focos, e as assíntotas dessa hipérbole.
Essa equação hiperbólica tem o feeling de uma equação hiperbólica com centro fora da origem. E esse tipo de equação tem a seguinte equação característica:
Para uma hipérbole horizontal, que tem o foco em onde e vértices e além disso, tem suas assíntotas em.
Ou:
Para uma hipérbole vertical, que tem o foco em onde e vértices e além disso, tem suas assíntotas em.
Temos que deixar então a expressão dada com a cara de alguma dessas, para isso vamos organizar com e com .
Somente de fazer isso já conseguimos ver que é uma hipérbole vertical.
Passo 2
Dessa forma a parcela parece muito com:
Logo basta somar no fator dentro do parenteses para resolver esse problema.
Agora para temos absolutamente a mesma coisa haha
Então basta somar dentro dos parênteses, o que nos deixa com a seguinte equação:
Por isso que não se pode já ir somando dos dois lados, a constante fora dos parênteses afeta bastante na função:
Agora vamos dividir por os dois lados:
O que nos diz que na verdade é uma hipérbole horizontal.
Vejam jojo’s bizarre adventure, por favor
Passo 3
Veja que quando temos uma equação com os termos:
E
O centro dela é então:
Essa equação nos diz que o centro dessa hipérbole está em:
Temos então:
E a nossa é:
Dessa forma:
E
E
E as assíntotas dessa função serão:
Os vértices (por ser uma hipérbole horizontal) serão iguais a:
Logo:
E o foco:
Logo:
Dessa forma o gráfico da função será:
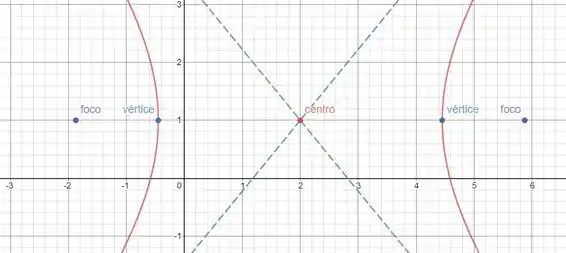
Resposta
Assíntotas:
Vértices:
Foco: