Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 22

No exercício a seguir, ache a equação da hipérbole com as propriedades dadas e faça um esboço do gráfico.

Focos em (-5,1) e (1,1) e um vértice em (-4,1)

Passo 1

É importante nessa questão, a gente fazer alguns esboços durante as resoluções, vai nos dá um bom norte sobre as equações! A primeiro momento, a gente percebe que os focos estão no mesmo eixo (eixo x), portanto a hipérbole tem um formato parecido com esse:

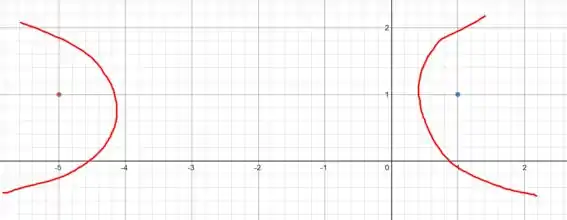
A questão também nos dá que existe um vértice em (-4,1), que fica no lado esquerdo da nossa hipérbole. E isso é absolutamente INCRIVÉL!! Sabe porquê? Porque a gente vai saber a distancia do foco até o vértice!

Se essa é a distância de um foco para um vértice de um lado, essa mesma distância vale para o outro foco:

Logo,

Com isso obtemos a distância entre os vértices, que é igual ao famoso 2a.

Passo 2

Olhe só!! Temos o valor de c e isso é um ótimo começo. E como dito anteriormente, os focos estão no mesmo eixo (eixo dos y), logo o maior vértice é também no eixo dos y. Tá mas... e agora? Vamos para a próxima info que eles nos deu: e comprimento do semi-eixo menor é três quartos do comprimento do semi-eixo maior. Isso me lembra uma equação... não lembra?

E segundo a info:

Portanto temos que:

Para achar o valor de a, vamos achar as raízes dessa eq. do segundo grau, vai ser rapidinho!

O foco dessa questão é geometria analítica, então vamos pular a parte e ir direto para as raízes e isolar a única raiz positiva (pois esse a se refere a uma distancia, e não existe distancia negativa, pelo menos não nesse universo!)

Portanto,

Passo 3

Uhuuuuul! Temos os valores de a,b e c!! Agora é so partir pro abraço! Sabemos que a equação de uma elipse (com eixo pararelo ao eixo y MAIOR) é igual a:

Em que Xc e Yc correspondem respectivamente as coordenadas x e y do centro da elipse. Pelas informações que a gente já tem, sabemos que o nosso centro fica na posição (-3,4). Portanto nosso Xc = -3 e nosso Yc = 4. Vamos montar a equação e nos livrar dessa questão? SIMBORA!

Organizando os dados: a = 2.3 , b = 1.725, Xc = -3, Yc = 4.

Logo, a nossa equação é: