Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.6 - Ex. 17
17- a) Encontre a excentricidade e a diretriz da cônica e plote a cônica e sua diretriz.
b) Se a cônica girar no sentido anti-horário ao redor da origem por um ângulo , escreva a equação resultante e plote sua curva.
Passo 1
Fala ai! Vamos lembrar de um teorema importante citado no livro que vai nos ajudar a resolver essa questãozinha.
a) Teorema 6:
Equação polar tem a forma.
Lembrando que é a excentricidade.
Note que o denominador está como então temos que transformar esse denominador de modo que temos a soma de 1 com algum fator trigonométrico.
Vamos dividir a equação por no numerador e no denominador para conseguirmos conhecer os parâmetros dessa cônica.
Precisamos colocar o numerador na mesma estrutura no do denominador. Então
Dessa forma a excentricidade valerá:
Passo 2
Pelo sinal negativo do cosseno nos dá a equação igual a:
Pelo denominador estar com uma função seno então sabemos que a diretriz é uma reta e por ser positiva sabemos que ela é um valor de positivo, logo a equação da reta diretriz vale:
Passo 3
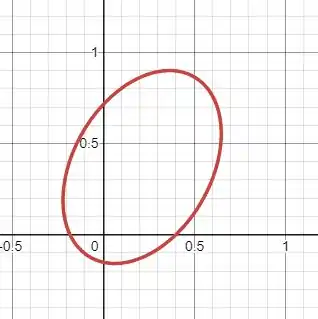
Gráfico:
Curva em azul é a reta diretriz e a curva vermelha a cônica.
Passo 4
Para rotacionar em nós precisaremos somar o ângulo dentro do cosseno de modo que teremos a seguinte equação:
Logo o gráfico ficará como:
