Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 8

Encontre o volume do sólido obtido pela rotação da região delimitada pelas curvas dadas em torno das retas especificadas. Esboce a região.

y = 1 4 x 2 ,   y = 5 - x 2 ; e m   t o r n o   d o   e i x o   x

Passo 1

Opa, bora resolver esse problema! O enunciado nos dá as seguintes curvas:

y = 1 4 x 2 ,   y = 5 - x 2

E pede pra a gente calcular o volume do sólido obtido pela rotação em torno do eixo x da região delimitada pelas curvas acima! Depois disso temos que esboçar a região!

Antes de qualquer coisa a gente precisa conseguir visualizar o problema. Então vamos esboçar o gráfico das curvas dadas. Temos duas parábolas onde:

y = 1 4 x 2 → c o n c a v i d a d e   p r a   c i m a ,   p a s s a   p e l a   o r i g e m

y = 5 - x 2 → c o n c a v i d a d e   p r a   b a i x o

Vamos calcular os pontos de intersecção entre as curvas:

1 4 x 2 = 5 - x 2

5 4 x 2 = 5

x = 4 = ± 2

Agora sim podemos plotar:

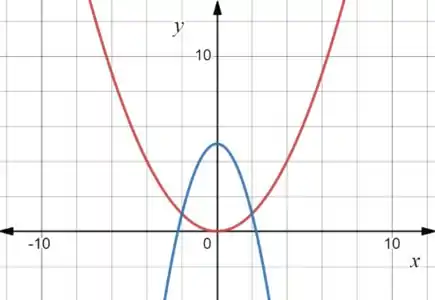
Passo 2

Uma área de disco circular (região entre 2 curvas) é calculada por:

A x = π R 2 - π r 2

Onde os raios aqui são as alturas de cada curva.

Substituindo as nossas curvas:

A x = π 1 4 x 2 2 - π 5 - x 2 2

A x = π 5 - x 2 2 - π 1 4 x 2 2

Assim,

A x = π 25 - 10 x 2 + x 4 - 1 16 x 4

O volume é a integral dessa área aí!

E os limites de integração são os pontos em que as parábolas de cruzam.

Passo 3

Temos então a seguinte integral:

V = ∫ - 2 2 A ( x ) d x

V = ∫ - 2 2 π ( 25 - 10 x 2 + 15 16 x 4 ) d x

Essa integral pode ser dividida em duas partes, devido os intervalos iguais, então

V = 2 π ∫ 0 2 25 - 10 x 2 + 15 16 x 4 d x

Resolvendo a integral, temos:

V = 2 π 25 x - 10 3 x 3 + 3 16 x 5 0 2

V = 2 π 25 × 2 - 10 3 2 3 + 3 16 2 5 - [ 25 × 0 - 10 3 0 3 + 3 16 0 5 ]

V = 2 π 50 - 80 3 + 6

V = 176 3 π

Passo 4

Agora a gente desenha a região:

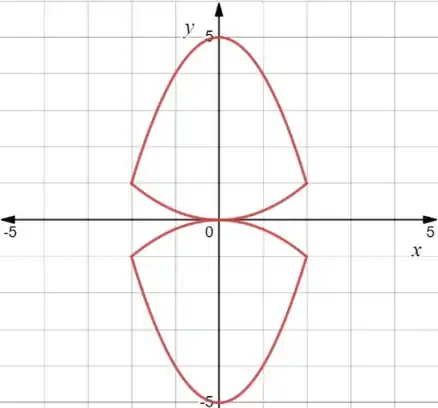
Prontinho!

Resposta

V = 176 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = t g 3 x ,y = 1 ,x = 0 ; e mt o r n od oe i x
Escreva, mas não calcule, uma integral para o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno da reta especificada. y = 0 ,y = s e n x ,0 ≤ x ≤ π ; e mt o r n od oy
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
A região delimitada pelas curvas y = e - 1 x , y = 0 , x = 1 e x = 5 é girada em torno do eixo x . Use a Regra de Simpson com n = 8 para estimar o volume do sólido resultante.