Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 7.7 - Ex. 41

A região delimitada pelas curvas y = e - 1 x , y = 0 , x = 1 e x = 5 é girada em torno do eixo x . Use a Regra de Simpson com n = 8 para estimar o volume do sólido resultante.

Passo 1

Vamos plotar as curvas:

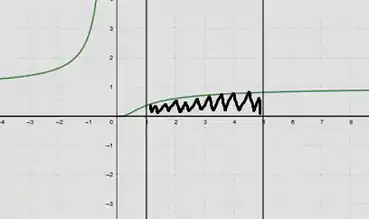
Para achar o volume vamos usar a fórmula:

V = ∫ 1 5 π e - 1 x 2 d x = π ∫ 1 5 e - 2 x d x = π I 1

Temos o intervalo 1 ≤ x ≤ 5 , e vamos usar n = 8 , temos que ∆ x :

∆ x = b - a n = 5 - 1 8 = 1 2

Com a Regra de Simpson é usado parábolas ao invés de segmentos de reta para aproximar a curva, assim a fórmula fica com um padrão 1 , 4 , 2 , 4 , 2 , . . . , 4 , 2 , 4 , 1 :

S n = f x 0 + 4 f x 1 + 2 f x 2 + 4 f x 3 + ∙ ∙ ∙ + 2 f x n - 2 + 4 f x n - 1 + f x n ∆ x 3

I 1 = S 8 = f 1 + 4 f 1,5 + 2 f 2 + 4 f 2 , 5 + ∙ ∙ ∙ + 2 f 4 + 4 f 4,5 + f 5 1 3 ∙ 1 2 ≈ 1,909433

Voltando a fórmula do volume:

V = π I 1 = 2 π 1,909433 ≈ 6

Resposta

O volume estimado do sólido resultante é de 6 unidades cúbicas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = 2 y + 1 x = 0 y = 0 y = 3
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = 2 y y 2 + 1 x = 0 y = 1
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = sec ⁡ x y = 2 - π 4 ≤ x ≤ π 4
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo y x = 2 sen ⁡ 2 y 0 ≤ y ≤ π 2 x = 0
Determine o volume dos sólidos obtidos com a rotação das regiões limitadas pelas retas e curvas em torno do eixo x y = sec ⁡ x y = tg ⁡ x x = 0 x = 1